RIST TUS

Division of Joint Research of Geometry

and Natural Science 　　　　　　　　　
　

ABOUT

　In this research division, we aim to construct the comprehensive geometric theory for the quantum mechanics, the condensed matter physics, molecular biology and grain boundary-composite materials mechanics, and feedback it to the above four fields. The geometry is divided broadly into three fields of the differential　geometry, the topology and the algebraic geometry. In the differential geometry, it was originally aimed to research a differential manifold M equipped with a geometric structure g (where a differentiable manifold means the space where the continuity and the differentiability of maps between the spaces can be defined) and investigate the properties of figures in the space (M,g) which are invariant under transformations of M preserving g invariantly. Note that the whole of such transformations of M preseriving g invariantly is a Lie group (that is, a differentiable manifold equipped with a suitable group structure). Later, in the differential geometry, it also has been aimed to research the theory of the connections of principal bundles and vector bundles over the space (M,g) in order to research the gauge theory (in the thoretical physics) from the viewpoint of the differential geometry. For example, the theory uinfying the gravitational field and the electromagnetic field is researched on the principal bundle having the unitary group U(1) of degree one as the structure group over a 4-dimensional Lorentzian manifold (M,g). Thus the differential geometry is closely connected to the theory of Lie group actions and the gauge theory, and hence can be applied to the researches of the quantum mechanics and the condensed materials physics. 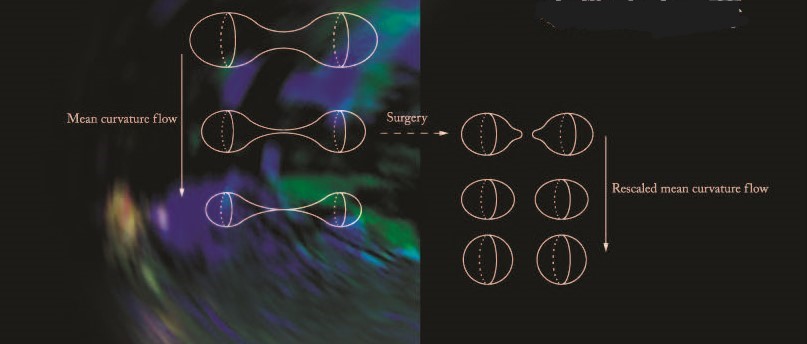In the geometric analysis (which is researched using both the differential geometry and the analysis), the mean curvature flow and the harmonic flow etc. are researched, where the mean curvature flow means the gradient flow of the (-1)-multiple of the volume functional, and the harmonic flow means the gradient flow the (-1)-multiple of the (usual) Energy functional). We aim to apply these researches to those of the grain boundary and the cluster. Also, we aim to apply these researches to that of the shape of double helices of polydeoxyribonucleotides constructing DNA etc. in the molecular biology. Furthermore, we aim to apply the research of the strength of the grain boundary to that of the composite materials mechanics.
　The topology aims to research a toplogical space X (where can be defined the continuity of maps between the spaces) and investigate the properties of the figures in X which are invariant under continuous transformations of X. Also, the various algebraic topological invariants (for example, the homotopy group and the homology group) are used in this research. The knot theory is very important in the research field of the topolgy and the research of DNA・RNA. The kont means a circle S^1 continuously embedded into the 3-dimensional sphere S^3 (or the 3-dimensional Euclidean space R^3). Here we note that knots in R^3 are regarded as knots in S^3 because R^3 is identified with an open portion of S^3. Main research thema of the knot theory is to investigate whether two knots in S^3 are mapped to each other by a homeomorphism of S^3 (=a continuos one-to-one map of S^3 onto oneself such that its inverse also is continuous). The knot theory is important in the research of the topoloogical global structure (the structure of double helices) of polydeoxyribonucleotides constructing circular DNA (in the molecular biology). Also, knots and the mapping class group are sometimes researched by using the gauge theory, which is one of so-called the topological field theory.
　In the algebraic geometry, are researched the structure of the common sero-point set of some polynomials over the affine space or the projective space. This research is used to investigate the moduli space of the space of various kind of connections of the principal bundle and hence is applied it to various reseaches of the gauge thoery.
　As above, each research field of the geometry are connected closely to those of the quantum mechanics, the condensed matter physics, molecular biology and grain boundary-composite materials mechanics. In detail, we aim to perform the following four researches.

I．The research of the condensed matter physics in the view-point of the gometric varitional theory
　The members of this reserach group aim to perform the following researches. In the sequel, the cluster means the cluster material composed of some atoms connected by the metallic bond, the covalent bond and the ionic bond. We grasp such a cluster material as a graph with the weight and the color, where the vertices implies the atom nucleuses of the atoms constructing the cluster material, they are connected by an edge in the case where two vertices (the atom nucleus) are binded and the weights are given to edges of the graph according to the degree of the bond strengths and the colors are given to vertices of the graph according to the structure of the atom having the vertex as the atom nucleus. Denote by V(G) the set of all vertices of the graph G and E(G) that of all edges of G. The graph G is defined as the pair (V(G),E(G)) precisely. For two v,w∊V(G), when there exists the edge connecting v and w, we denote it by |vw|. Also, denote by m(e) the weight of e:=|vw| and C(v) the color of v. Denote by |\vec{vw}| the edge e:=|vw| given the orientation going from v to w and |\vec{wv}| the edge e:=|vw| given the orientation going from w to v, where |\vec{vw}| denotes the notation given → on |vw| and |\vec{wv}| also is similar. The correpondence O defined by assigning an orientation O(e) of e to each edge e∊E(G) is called an orientation of G. The quadruple (G,m,C,O) is called an oriented graph with weight and color.
　For an oriented graph (G,m,C,O) with weight and color, denote by |G| the sum of all edges of G. Note that |G| is not embedded into 3-dimensional Euclidean space R^3 yet. It is important to investigate how the shape of the cluster material is in R^3, that is, how |G| is imbedded into R^3. We plan to investigate the shape of the cluster material in R^3 from the view-point of the geometric variational theory as follows. Denote by Map_{PS}(|G|,R^3) the space of all piecewise smooth maps of |G| into R^3. Take a suitable energy functional E_{m,C} (over Map_{PS}(|G|,R^3)) depending on the structure of |G|, the weight anf the color and find critical points of -E_{m,C}. Let f(∊Map_{PS}(|G|,R^3)) be one of the critical points. Then we interpret that f(|G|) is the shape of the stable state of the cluster material in R^3.
　Also, we define a fibre bundle π:E → R^3 over R^3 depending on the color C and plan to investigate the shape of |G| in the total space E. We plan perform this investigation as follows. Denote by Map_{PS}(|G|,E) the space of all piecewise smooth maps of |G| into E. Take a suitable energy functional E_m (over Map_{PS}(|G|,E)) depending on the structure of |G| and the weight and find critical points of -E_m. Let f(∊Map_{PS}(|G|,E)) be one of the critical points. Then we interpret that f(|G|) is the shape of the stable state of the cluster material in E.
　Furthermore, we plan to define a suitable subdivision of an oriented graph with weight and color and investigate whether the analoguous space obtained by repaeting to take this subdivision in infinite time is a Riemannian manifold with affine connection (or in more general, a measured metric space with a connection). Here a Riemannian manifold with affine connection means a manifold M equipped with a Riemannian metric g and an affine connetion ∇ on M, where g is a (0,2)-tensor field on M defined by assigning an inner product g_p of the tangent space T_pM of M at p to each p∊M) and an affine conncection ∇ (which defines the parallel translation P_c:T_{c(0)}M → T_{c(1)}M along each curve c:[0,1] → M), and a measured metric space with a connection means a metric space equipped with a measure and a kind of connection (defining the parallel translations along a kind of continuous curves).

II.　The research of the quantum walk in the view-point of the gometric gauge theory
　The members of this reserach group aim to perform the following researches.
The gauge theory in the differential geometry is discussed by using the connections on a principal bundle π:P → M having a compact semi-simple Lie group H as the structure group over a Riemannian manifold (or a Lorentzian manifold) and the associated vevtor bundle π_ρ:P×_ρC^n → M for a representation ρ:H → GL(n,C).
Here the total space P of the principal bundle π:P → M is almostly equal to the product manifold M×G and the total space E_{P,ρ}:=P×_ρC^n of the vector bundle h_ρ:P×_ρC^n → M is almost equal to M×R^n.
　The time evolution of quantum states on a Riemannian manifold (M,g) is given as a solution of the Schrōdinger equation (or the Dirac equation) defined by using a Hermitian operator H from the Hilbert space Γ(E_{P,ρ}) of all L^2-cross sections of the vector bundle h_ρ:E_{P,ρ} → M to oneself. Here we note that Γ(E_{P,ρ}) implies the space of all quantum states and H is defined by using a suitable Hamiltonian on E_{P,ρ}.
　On the other hand, the time evolution of quantum states on an oriented graph (G,m,C,O) with weight and color is given as a solution of the the discretized Schrōdinger equation (or the discretized Dirac equation). The discretized Schrōdinger equation is given as a time-continuous and space-discrete equation and the solution is called a time-continuous quantum walk. Also, the discretized Dirac equation is given as a time-discrete and space-discrete equation and the solution is called a time-discrete quantum walk.
　The members of this research group aim to define a discretized Schrōdinger equation and the discretized Dirac equation suitably by using the weight m and the color C, and investigate the behaviours of the time-continuous quantume walk and the time discrete quantum walk.

III.　The research of DNA・RNA in the view-point of the knot theory, the topological field theory and the gometric varitional theory
　The members of this research group aim to perform the topological research and the differential geometrical research of circular DNA・RNA's
　A DNA is constructed by two polydeoxyribonucleotides and base pairs connecting them. If the DNA is circular, then the two polydeoxyribonucleotides form a link in R^3 (hence S^3). A RNA has the structure removed one of two polydeoxyribonucleotides constructing a DNA and a polydeoxyribonucleotide forms a knot in R^3 (hence S^3). The topological research of circular DNA・RNA's means to investigate the change of the exitrinsic topological structures of the link and the knot by enzymes. On the other hand, the differential geometrical research of circular DNA・RNA's means to investigate the shapes (in R^3) of double helices formed by two polydeoxyribonucleotides constructing a circular DNA and a helix formed by a polydeoxyribonucleotide constructing a circular RNA.
　In detail, we aim to perform the following researches. First we aim to explain theoretically the mechanism where the recombinant DNA, the transcription (the process synthesizing RNA from DNA) and the translation of RNA into protein arise by the enzymes. These processes are topological changes. We aim to find the new methods controling these topological changes from the view-points of the molecular biology, the nucleic acid biology and the topology (in particular, the knot theory and the mapping class group theory the topological field theory).
　 DNA is a polymer consisting of the oxygen O，the phosphorus P，the hydrogen H，the nitrogen N，the methylene CH_2，the hydroxyl group OH and the oxide ion O^- and this is grasped as an oriented graph with the weight, the measure and the color. Denote by (G,O,m,μ,C) this orieted graph with the weight, the measure and the color. We define the energy functional E_{m,μ,C} suitably by using the structure of the graph, m, μ and C, and calculate a ciritical point f of this functional. Then the image f(|G|) is interpreted as one of stable shapes of the DNA in R^3. We aim to analyze theoretically the shape of double helices constructed by two polydeoxyribonucleotides in the stable shape o f the DNA in R^3.
　The gauge theory (the quantum field theory) to calculate various topologival inavariants is called the topologial field theory. The Chern-Simons theory is a representative topological field theory. The Chern-Simons theory is as follows. There exists a Jones polynomial (which we denote by J(k)) as one of topological invariants of of a knot K in the 3-dimensional sphere S^3. The Chern-Simons theory is the topological field theory to describe this topological invariant J(K) by using some functional (which is called the Chern-Simons functional) defined on the space of all connections of a SU(2)-bundle over S^3 and the quantity called the Wison loop given by the holonomy of a connection of the SU(2)-bundle along K. Here we note that, since S^3 is grasped as the space given by laminating two 3-dimensional closed balls B^3's along their boundariesy and the interior of B^3 is identified with R^3, knots in R^3 are regaraded as knots in S^3.
　For the pair (K_1,K_2) of the knots given by two polydeoxyribonucleotides constructing the original DNA, if it is shown by using the above descrptions of J(K_i) that the Jones polynomial J(K_i) must be changed by some enzymes, then each knot K_i must be surgeried. This surgery is called a band surgery. Thus the Chern-Simons theory is possible to be applied to the research of the extirinsic topological changes of the DNA by enzymes.

IV.　The research of the grain boundary in the view-point of the geometric analysis and its application to the composite materials mechanics
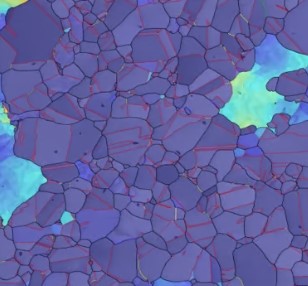
　The members of this research group aim to perform the following research. The grain boundary means the interfaces between grain crystals forming polycrystalline.
　First we aim to research the method to controlling the shape of the grain boundary by analyzing the grain growth in terms of the phase-field method. Also, we aim to investigate the strength of the grain boundary and furthermore apply it to the composite materials mechanics. We shall graspe the process where the polycrystalline is formed as follows. We consider the process is divided into the following two steps. The first step is the process that many tiny grains are generated and grows up by cooling liquids. As the result, a polycrystalline with unstable grain boundary is formed. We aim to research this step as the time evolution of a phase field function along the gradient flow of the (-1)-multiple of suitably modified free-energy functional Ginzuburg-Landau-type evolution equation. The second step is the process that the unstable grain boundary converges to a stable grain boundary along the gradient flow of the (-1)-multiple of some suitably defined energy functional E. Note that this stable grain boundary is a critical point of －E. Furthermore, we aim to find a method to analyze in detail the strength of the stable grain boundary and apply its analysis to the composite materials mechanics.
　Secondly, we aim to research the analoguous model of the polycrystalline. Grains constructing polycrystalline are grasped as oriented graphs with weight and color. Hence the polycrystalline is a family of such oriented graphs. Let {(G^a,m^a,C^a,O^a)}_{a=1}^k be the family and set S^{ab}:=|G^a|⋂|G^b| when |G^a|⋂|G^b| is not empty. Then the grain boundary S of this polycrystalline is the sum of S^{a,b}'s. Let |G| be the sum of |G^a| (a=1,..,k} and Map_{PS}(|G|,R^3) the space of all PS-maps from |G| to R^3. According to the structure of the crystalline, we take suitable subdivisions of G^a (a=1,...,k). Denote by G^a_1 (a=1,...,k) this subdivision. In the sequel, by repeating this process to take such a subdivision infinite times, a sequence of subdivisions {G^a_i}_{i=1}^∞ of G^a (a=1,...,k) is obtained. Furthermore, we define a sequence {(G^a_i,m^a_i,C^a_i)}_{i=1}^∞ of oriented graphs with weight and color. We aim to investigate whether this sequence (or this subsequence) converges to some analoguous space (for example, a 2-dimensional (or 3-dimensional) piecewise smooth manifold with a Riemannian metric and a affine connection (M_a,g_a,∇^a). Let |G_i| be the sum of |G^a_i|'s (a=1,..,k} and M be the sum of M_a's (a=1,...,k). Denote by Map_{PS}(M,R^3) the space of all PS-maps. We take a suitable energy functional E_i depending on {m^a_i}_{a=1}^k, {C^a_i}_{a=1}^k、the shapes of the grain boundaries S_i of |G_i|'s and how to join of G^a and G^b along S_i^{ab}, and find a sequence {f_i}_{i=1}^∞ critical points of E_i's such that converges to some f_∞ (∊Map_{PS}(M,R^3)) as i → ∞. Furthermore, we plan to investigate whether f_∞ is a critical point of suitably chosen energy functional E_∞:Map_{PS}(M,R^3) → R depending on g_a and ∇^a (a=1,...,k). 、In the above method, we aim to construct an analogous model of polycrystalline.

　　　Professor Naoyuki Koike (Director of DGNS)
　　　 　　　　

　　　
　　　　I.　Crystal Structure 　　　　　　　　　　　II.　Quantum State

　　　
　　　　　 　 III.　DNA 　　　　　　　　　　　　　　 IV.　Grain Boundary