1-2 Electrostatic Potential(静電ポテンシャル)
逆2乗則を持つベクトル場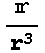 は
は
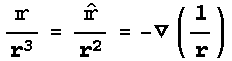
の様に、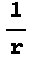 というスカラー場のGradientとして表すことができ、より一般に原点を
というスカラー場のGradientとして表すことができ、より一般に原点を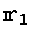 に移せば
に移せば
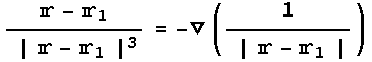
と書ける。(ここでGradient演算子は座標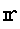 に作用することに注意) この算術(物理ではなく数学)を、先に与えた電場の表式
に作用することに注意) この算術(物理ではなく数学)を、先に与えた電場の表式
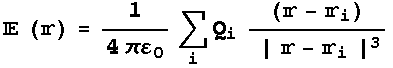
に用いて、電場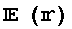 を、スカラー場
を、スカラー場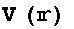 のGradientとして
のGradientとして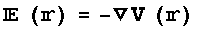 の形で表すことができ、
の形で表すことができ、
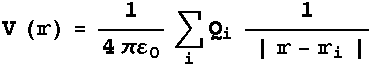
と書ける。このスカラー場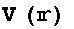 を点電荷
を点電荷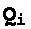 の集まりによる「静電ポテンシャル(Electrostatic Potential)」[あるいは電位]と呼ぶ。
の集まりによる「静電ポテンシャル(Electrostatic Potential)」[あるいは電位]と呼ぶ。
●電場のベクトル量としての重ね合わせが、ポテンシャルのスカラー量としての可算性として表されている。このことは、与えられた電荷分布による電場を直接計算するよりは、まずポテンシャルを求めた後、そのGradientをとることにより電場を計算したほうが簡単な場合があることを意味している。
●この静電ポテンシャル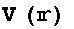 は任意の定数を加えてもそのGradientとしてして導かれる電場は同じでありポテンシャルの基準点は考える問題に応じて都合の良いように選ぶことができる。(力学のポテンシャルエネルギーと同様) ここに与えられた
は任意の定数を加えてもそのGradientとしてして導かれる電場は同じでありポテンシャルの基準点は考える問題に応じて都合の良いように選ぶことができる。(力学のポテンシャルエネルギーと同様) ここに与えられた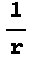 の静電ポテンシャルは、電場の源である点電荷
の静電ポテンシャルは、電場の源である点電荷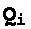 の集まりから無限遠方に離れた場所でzeroになるようなポテンシャル基準を選んでいる。
の集まりから無限遠方に離れた場所でzeroになるようなポテンシャル基準を選んでいる。
●この基準のもとでは、静電ポテンシャルは、電場の源である点電荷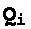 の集まりから無限遠方に離れた場所から、単位電荷を,位置
の集まりから無限遠方に離れた場所から、単位電荷を,位置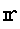 に移動させるために必要なエネルギーを表している。
に移動させるために必要なエネルギーを表している。
●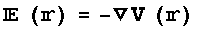 についてRotationを取ると任意の点でzeroになり静電場は渦無し場の条件
についてRotationを取ると任意の点でzeroになり静電場は渦無し場の条件
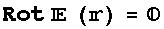
を満たす。(これは静電場に対するMaxwell方程式の一つである)
.gif)
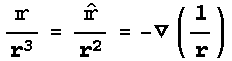
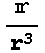 は
は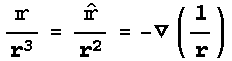
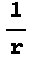 というスカラー場のGradientとして表すことができ、より一般に原点を
というスカラー場のGradientとして表すことができ、より一般に原点を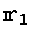 に移せば
に移せば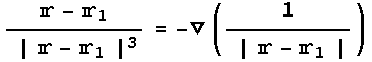
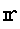 に作用することに注意) この算術(物理ではなく数学)を、先に与えた電場の表式
に作用することに注意) この算術(物理ではなく数学)を、先に与えた電場の表式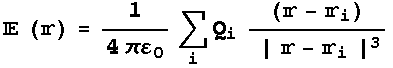
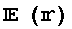 を、スカラー場
を、スカラー場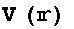 のGradientとして
のGradientとして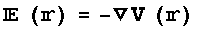 の形で表すことができ、
の形で表すことができ、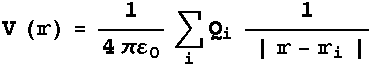
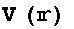 を点電荷
を点電荷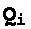 の集まりによる「静電ポテンシャル(Electrostatic Potential)」[あるいは電位]と呼ぶ。
の集まりによる「静電ポテンシャル(Electrostatic Potential)」[あるいは電位]と呼ぶ。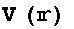 は任意の定数を加えてもそのGradientとしてして導かれる電場は同じでありポテンシャルの基準点は考える問題に応じて都合の良いように選ぶことができる。(力学のポテンシャルエネルギーと同様) ここに与えられた
は任意の定数を加えてもそのGradientとしてして導かれる電場は同じでありポテンシャルの基準点は考える問題に応じて都合の良いように選ぶことができる。(力学のポテンシャルエネルギーと同様) ここに与えられた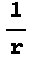 の静電ポテンシャルは、電場の源である点電荷
の静電ポテンシャルは、電場の源である点電荷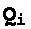 の集まりから無限遠方に離れた場所でzeroになるようなポテンシャル基準を選んでいる。
の集まりから無限遠方に離れた場所でzeroになるようなポテンシャル基準を選んでいる。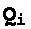 の集まりから無限遠方に離れた場所から、単位電荷を,位置
の集まりから無限遠方に離れた場所から、単位電荷を,位置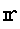 に移動させるために必要なエネルギーを表している。
に移動させるために必要なエネルギーを表している。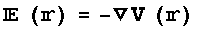 についてRotationを取ると任意の点でzeroになり静電場は渦無し場の条件
についてRotationを取ると任意の点でzeroになり静電場は渦無し場の条件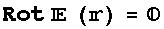
.gif)