
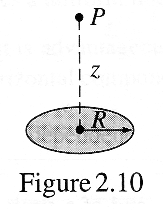


<解説>
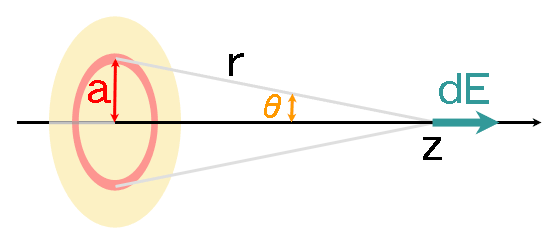

これは、zの正負に関わらず、|z|>0で成り立つことに注意してください。
この様子をグラフに表すと、
→Mathematica file
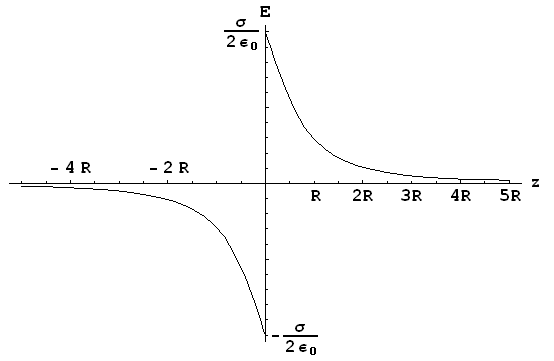
となります。zが0に近づくほど電場はσ/2ε0に近づいていきます。
このこと、もしくは(2.6.2)式でR→∞とすることによって、
無限大の平面が作る電場は距離zによらず
σ/2ε0であることがわかります。
それではz>>Rならどうなるでしょうか?円板の総電荷はσπR2
ですから…
となるはずですが…確認してみてください。
Q1:
ところで、z=0のときはどうなるのでしょう?
(求められた式でz→+0とz→−0が異なる結果になり、
不定になってしまいます!)
z=0のときは円板の中心での対称性から、E=0です。
そもそも円板に垂直な方向の電場成分はないのですから、(2.6.1)式の
ように考える点に問題があります。

(z=0では上図のようなdEは考えられない)
Q2:
Problem 2.5 (Textbook p64) を解いて、
Circular Loopによる電場を求めると、上で解いたCircular Disk
の時と異なり、原点(z=0)での不連続性がなくなりました。
なぜ0からRまで積分したCircular Diskでは不連続となるのでしょうか?
物理的にはどういうことなのでしょうか?…考えてみてください。

グラフを見ると、(オレンジがCircular Loop、
黒がCircular Diskです。)

のようになっていて、Representive Vectorsで表わせば、

のようになっています。(注:上のグラフと同じスケールではありません。)