 相転移の最も身近な例は「水・氷・水蒸気」の変化である。水は0度以下では固体である「氷」になり、0度以上100度以下では液体である「水」になり、100度以上では気体である「水蒸気」となる。それぞれ構成している分子(H2O)は同じであるが、そのマクロな性質は大きく異なる。このように同じ物質における、マクロな性質が異なる状態を「相(phase)」と呼び、相が変わる現象の事を「相転移(phase transition)」と呼ぶ。
相転移の最も身近な例は「水・氷・水蒸気」の変化である。水は0度以下では固体である「氷」になり、0度以上100度以下では液体である「水」になり、100度以上では気体である「水蒸気」となる。それぞれ構成している分子(H2O)は同じであるが、そのマクロな性質は大きく異なる。このように同じ物質における、マクロな性質が異なる状態を「相(phase)」と呼び、相が変わる現象の事を「相転移(phase transition)」と呼ぶ。物理学では相転移現象をどのように取り扱う事ができるだろうか?たとえばこの「水はなぜ凍るのか?」という問題に対して、学部2年までの間に学んだ力学や電磁気学を用いて答えを出す事はほとんど不可能である事は直感的に分かるであろう。これはアボガドロ数個のH2O分子一つ一つに運動方程式をたてて解決できる問題ではなく、「熱」「エントロピー」といった物理量を導入し統計的なアプローチを持って初めて記述できる問題である。 本実験課題では、コンピュータによるシミュレーションを通して、まずはこの「相転移」についての理解を深めてみよう。 |
 磁石同士が引き合ったり、反発し合ったり、磁石がクリップを引き寄せたりする事が磁力のためである事や、
その磁力の元は物質中の「磁気(双極子)モーメント」である事は電磁気学で既に学んだ通りである。
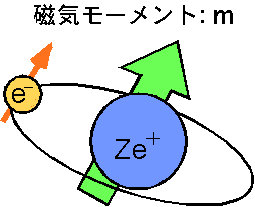
この磁気モーメントの起源をさらに微視的に見て行くと、実際の物質中では原子一つ一つがこれを担っている。
磁石同士が引き合ったり、反発し合ったり、磁石がクリップを引き寄せたりする事が磁力のためである事や、
その磁力の元は物質中の「磁気(双極子)モーメント」である事は電磁気学で既に学んだ通りである。
この磁気モーメントの起源をさらに微視的に見て行くと、実際の物質中では原子一つ一つがこれを担っている。



