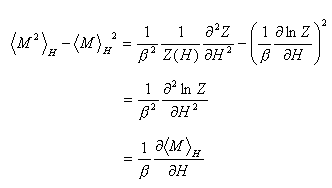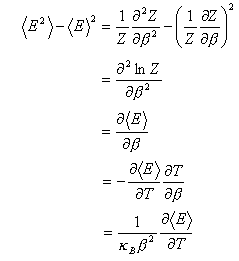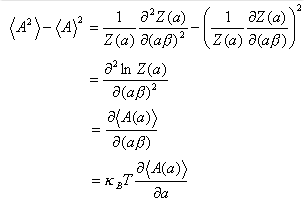AppendixB:揺らぎと応答(カークウッドの関係式)
[BACK]
[NEXT]
磁化�および磁化の 2 乗の熱平均値�は以下のように分配関数 Z により求められる.
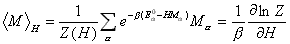
(B-1)
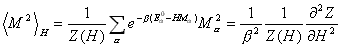
(B-2)
は外磁場が加わっていない時の状態αにおける全エネルギーである.
(B-1) 式,(B-2) 式から磁化の熱平均値のまわりのゆらぎ<(M-<M>H)2>Hを計算すると以下の様な関係式が得られる.
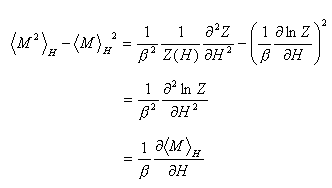
よって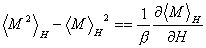
(B-3)
ここで外磁場H→0の極限を考え,(A-3) 式のゼロ磁場帯磁率の定義を思い起こせば,ゼロ磁場帯磁率 χ とゼロ磁場における磁化のゆらぎを関係づける
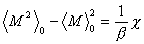
(B-4)
を得る.
ゼロ磁場における比熱 C とゼロ磁場における内部エネルギーのゆらぎの関係も同様にして求められる.
内部エネルギー<E>および内部エネルギーの 2 乗の熱平均値<E2>は以下のように分配関数 Z により求められる.
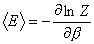
(B-5)
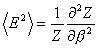
(B-6)
(B-5) 式,(B-6) 式から内部エネルギーの熱平均値のまわりのゆらぎ<(E-<E>H)2>Hを計算すると以下の様な関係式が得られる.
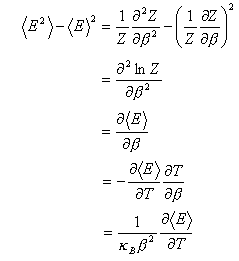
よって
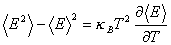
(B-7)
ここで (A-5) 式のゼロ磁場における比熱 C の定義を思い起こせば,ゼロ磁場における比熱 C とゼロ磁場における内部エネルギーのゆらぎを関係づける
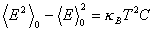
(B-8)
を得る.
一般には
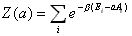
(B-9)
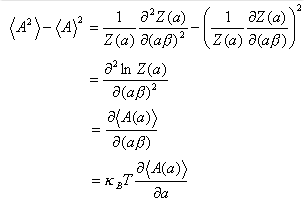
(B-10)
ゆえに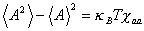
(B-11)
ここで
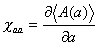
(B-12)
であり,一般的な力 a が変位 � を引き起こす応答率を表すものである.
このように (B-4) 式, (B-8) 式は,平衡状態の揺らぎと外力に対する応答の関係を表すものとみることができる.(カークウッドの関係,Kirkwood relation)
[BACK]
[NEXT]