AppendixD:Single Spin Flip メトロポリス法
[BACK]
[NEXT]
熱平衡状態におけるボルツマン分布Peqを持つように出現する状態αiをどのように生成すれば良いのであろうか? モンテカルロ法においては状態αiを、その一つ前の状αi-1のみから確率的に作るマルコフ鎖的な状態列{αi}を生成している。
状態αiから状態αjへの遷移確率ωαi→αjと状態αiから状αjへの遷移確率ωαi→αjに必要であるが十分過ぎる詳細釣り合いと呼ばれる条件ωαi→αjPeq=ωαj→αiPeqを課せば定常状態の分布を得ることができる。ボルツマン分布e-β[E(α)]の形から遷移確率ωαi→αjPeq=ωαj→αiPeqの比について次の関係が得られる。
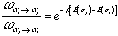
これを満たす限り、遷移確率ωαj→αiの選び方には自由度がある。
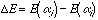 として、
として、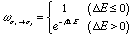
のように,ΔE<=0の場合はαiの状態を必ず採用し,ΔE>0の場合はe-βΔEの確率ではαiの状態を採用する方法をメトロポリス法という。状態αiから新しく状態αjを作る際に、1個の磁気モーメントを反転させた状態を次の新しい状態αjの候補として考えるためSingle Spin Flipによるメトロポリス法と呼ばれる。Single Spin Flipさせる格子点を次々と変えていく必要があるが、ここでは、タイプライタ-式にscanする方法を用いる。さて、このSingle Spin Flipによるメトロポリス法によって生成された状態列{αi}すべてを(2-3)式で表される熱統計平均に用いるべきであろうか?続いた状態はSingle Spin Flipのみの違いであり、状態空間内で極めて近距離にあり、強い相関を持っている。よってたとえばN個の格子点がすべてscanされる程度の間隔で隔てられた状態列のみを熱統計平均に用いるべきであろう。全格子点をScanし終えて次の新しい状態を生み出す手続きをOneMonteCaruloSweepと呼び、1 MonteCarulo Step(1MCS)進んだと表現する。この1MCSごとに必要な示量性の物理量をサンプリングする。

OneMonteCarulo Sweepの手続きは以下のフローチャートの様にまとめられる。
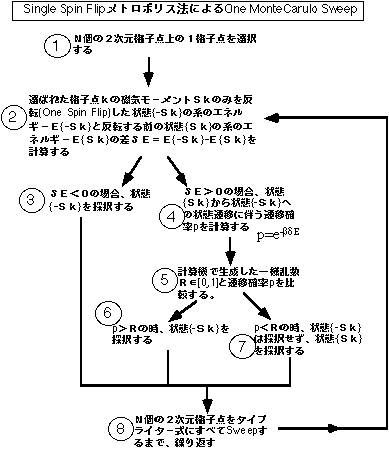
もう少し詳しい図をここに用意しておいたので興味ある人は見て欲しい。
参考書
1) シミュレーション物理学: D.W.ヘールマン著 (シュプリンガーフェアラーク東京)
2) 熱統計力学 (物理学基礎シリーズ4) 8章: 宮下精二 著 (培風館)
[BACK]
[NEXT]
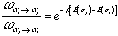
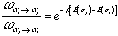
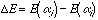 として、
として、