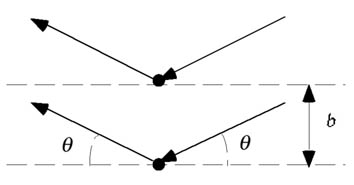
図4 Bragg反射
一次元方向に並ぶ原子による散乱を考えよう。
導入として、二本の原子棒からのBragg反射を見る。二本の原子棒からの反射波の位相差は(波数)×(光路差)で求めることが出来る。

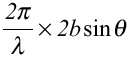
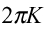 (Kは実数)・・・(1)
(Kは実数)・・・(1)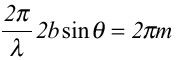 (mは整数)・・・(2)
(mは整数)・・・(2)
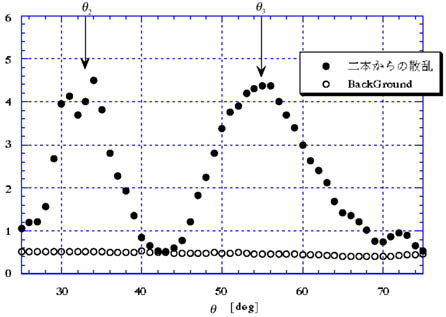
実験2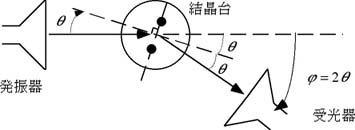
図5 二本の原子棒からの反射(格子定数b=6[cm]、波長λ=3.27[cm]) 図5の様に結晶台を、二本の原子棒を通る平面に垂直な平面が入射ビームとなす角がθとなるように、また受光器がψ=2θとなるように同時に動かして、入射角=反射角=θを設定する。ψ(=2θ)>50°なる範囲で測定するということを考慮に入れて、θを25°から75°まで1°間隔で変化させ、Intensityを測定せよ。 |
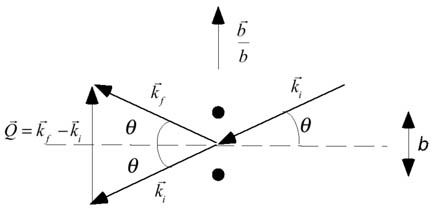
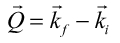
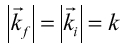 より図7から
より図7から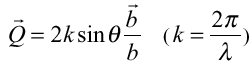 ・・(3)
・・(3)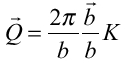 (Kは実数)・・・(4)
(Kは実数)・・・(4)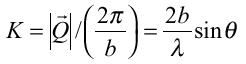
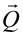 が
が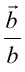 方向に
方向に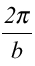 の整数倍の大きさを持てば反射波は強め合うことができる。この波数空間を逆格子空間といい、この空間における、
の整数倍の大きさを持てば反射波は強め合うことができる。この波数空間を逆格子空間といい、この空間における、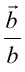 方向に
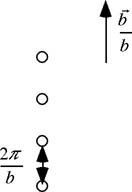
方向に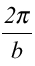 の整数倍になる位置を逆格子点という(図9)。また、逆格子点を指し示すベクトルは
の整数倍になる位置を逆格子点という(図9)。また、逆格子点を指し示すベクトルは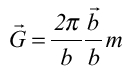 (mは整数)
(mは整数)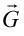 を逆格子ベクトルと呼ぶ。
を逆格子ベクトルと呼ぶ。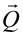 が逆格子ベクトル
が逆格子ベクトル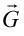 に一致
に一致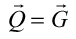
実験3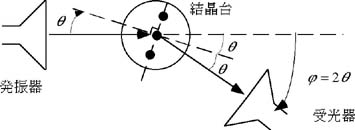
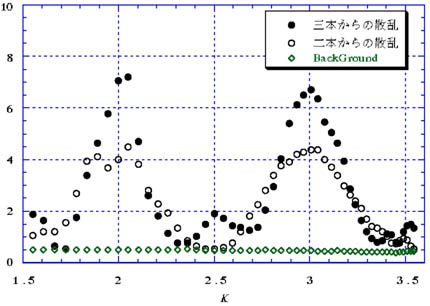
図10 三本の原子棒からの反射(格子定数b=6[cm]、波長λ=3.27[cm]) 実験2と同様に、原子棒を三本にして行え。 |
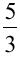 、K=
、K=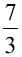 、K=
、K=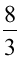 では位相差がそれぞれ
では位相差がそれぞれ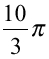 、
、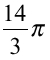 、
、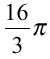 となり、三本は完全に打ち消し合う。
となり、三本は完全に打ち消し合う。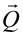 が
が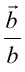 方向にあったため、
方向にあったため、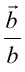 方向に並ぶ原子の周期により、強め合ったり、弱め合ったりしていた。では、
方向に並ぶ原子の周期により、強め合ったり、弱め合ったりしていた。では、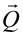 が
が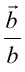 方向以外を向いたらどうなるだろうか。
方向以外を向いたらどうなるだろうか。
実験4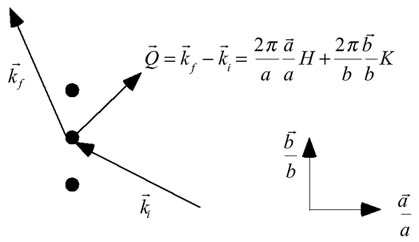
図12 散乱の様子(格子定数b=6[cm]、波長λ=3.27[cm]) 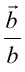 方向に直交する単位ベクトルを 方向に直交する単位ベクトルを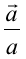 とし、散乱ベクトル とし、散乱ベクトル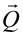 が が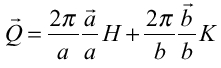 (H、Kは実数)・・・(5) (H、Kは実数)・・・(5)となるときの散乱(a は適当な正の実数で、便宜上 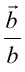 方向の係数とそろえて記述した)について、以下の実験を行え。 方向の係数とそろえて記述した)について、以下の実験を行え。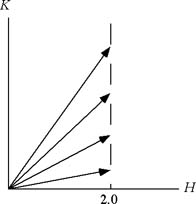
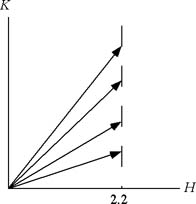
図13 図14 図13、図14 波数空間における 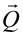 の変化 の変化
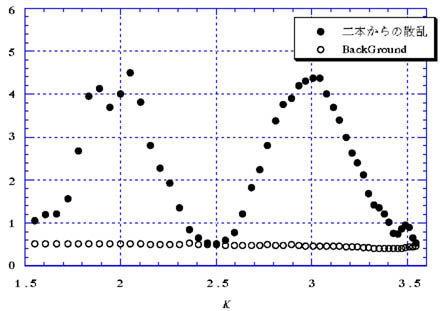
実験4_1図13の様に、H=2.0(a=6とする)としてKを0から3.0まで0.1ごとに変化させてIntensityを測定せよ((2 K)Scan)。
実験4_2図14の様に、H=2.2(a=6とする)としてKを0から2.8まで0.1ごとに変化させてIntensityを測定せよ((2.2 K)Scan)。設定は次の通り。 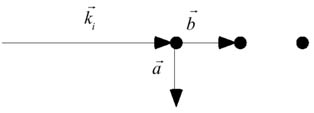
図15 初期設定 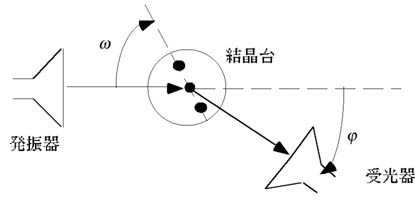
図16 測定の様子  方向を同一にして、その後Labviewに従って結晶台をω、受光器をψだけ回転させよ(図16)。 方向を同一にして、その後Labviewに従って結晶台をω、受光器をψだけ回転させよ(図16)。 |
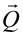 が(5)式において、Hの値によらずKが整数となっていれば強め合っているのが分かる。ある
が(5)式において、Hの値によらずKが整数となっていれば強め合っているのが分かる。ある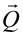 における、隣り合う原子棒からの反射波の位相差を調べてみよう。
における、隣り合う原子棒からの反射波の位相差を調べてみよう。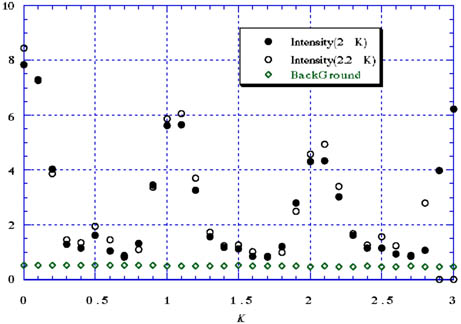
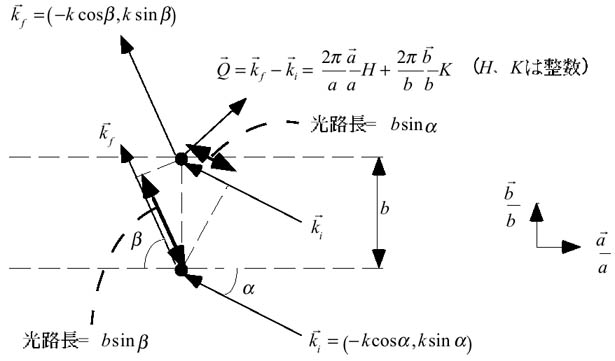
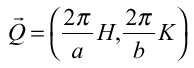
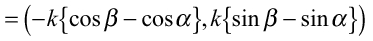
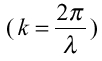 ・・・(6)
・・・(6)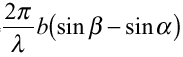 ・・・(7)
・・・(7)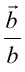 方向の成分を代入して
方向の成分を代入して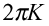 ・・・(8)
・・・(8)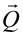 が図19の様に線上のどこかに位置すれば反射波は強め合う。これは
が図19の様に線上のどこかに位置すれば反射波は強め合う。これは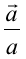 方向に周期性がないことに起因している。
方向に周期性がないことに起因している。
実験5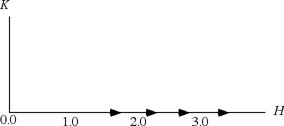
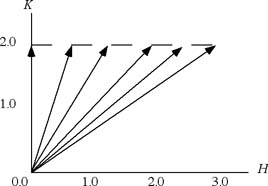
図20 図21 図20、図21 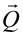 の変化 の変化
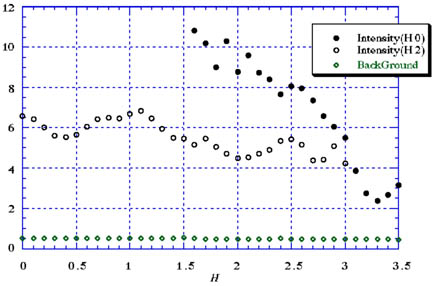
実験5_1図20の様に、K=0として(a=6とする)Hを1.6から3.5まで0.1ごとに変化させてIntensityを測定せよ((H 0)Scan)。
実験5_2図21の様に、K=2.0として(a=6とする)Hを0から2.9まで0.1ごとに変化させてIntensityを測定せよ((H 2)Scan)。実験3、実験4と同様に結晶台に原子棒を配置し(b=6[cm]、三本一列)、設定も実験4と同様に行え。 |
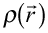 は
は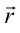 での散乱能)
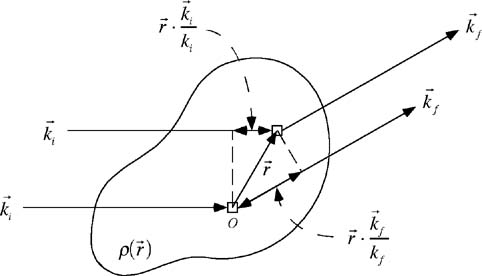
での散乱能)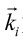 方向からの入射ビームが散乱体により
方向からの入射ビームが散乱体により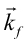 方向に散乱される(図23)。原点Oの面積素片とそこから
方向に散乱される(図23)。原点Oの面積素片とそこから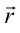 だけ離れた面積素片からの散乱波の干渉は位相差
だけ離れた面積素片からの散乱波の干渉は位相差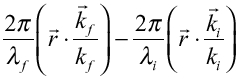
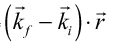
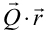
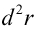 からの散乱波
からの散乱波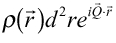 の散乱体全体からの重ね合わせを求めると
の散乱体全体からの重ね合わせを求めると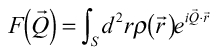 ・・・(9)
・・・(9)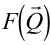 は散乱振幅と呼ばれ、散乱能
は散乱振幅と呼ばれ、散乱能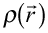 のFourier変換の形となっている。ところで、Intensityは受光器の特性により
のFourier変換の形となっている。ところで、Intensityは受光器の特性により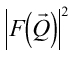 に比例する。つまり、観測されたIntensityは、散乱前後の波数ベクトル
に比例する。つまり、観測されたIntensityは、散乱前後の波数ベクトル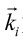 、
、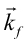 によって定まる
によって定まる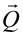 が指定する、散乱体のFourier変換におけるFourier成分
が指定する、散乱体のFourier変換におけるFourier成分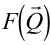 の絶対値の自乗
の絶対値の自乗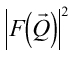 を表している。
を表している。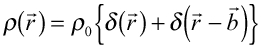 )
)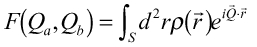
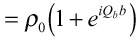
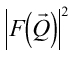 )は図24の様になる。
)は図24の様になる。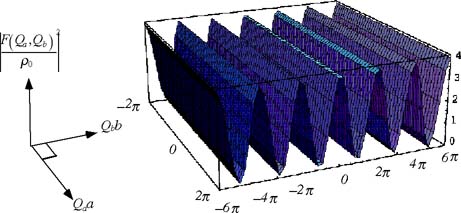
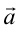 は
は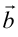 に垂直なベクトル)
に垂直なベクトル)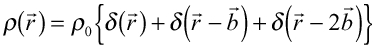 )
)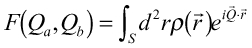
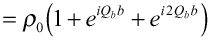
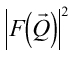 )は図25の様になる。
)は図25の様になる。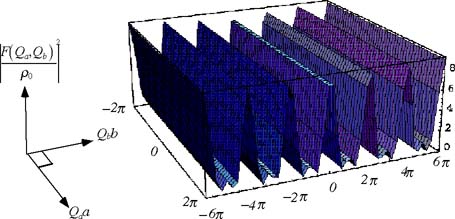
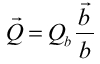
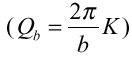
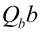 方向にScanしたことになる(図26、図27)。
方向にScanしたことになる(図26、図27)。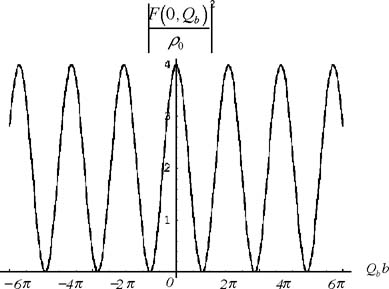
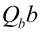 方向
方向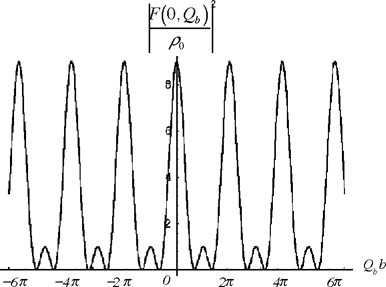
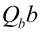 方向
方向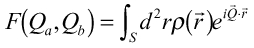
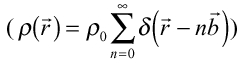
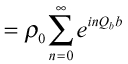
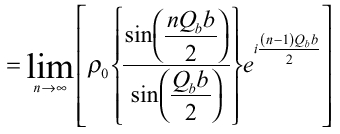
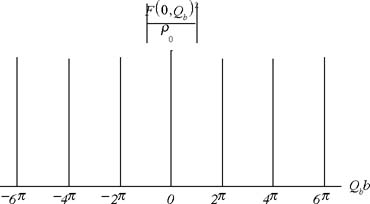
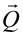 のみが存在する(Fourier級数)。
のみが存在する(Fourier級数)。