実験6
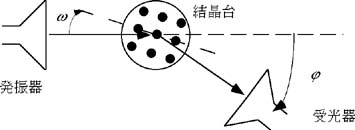
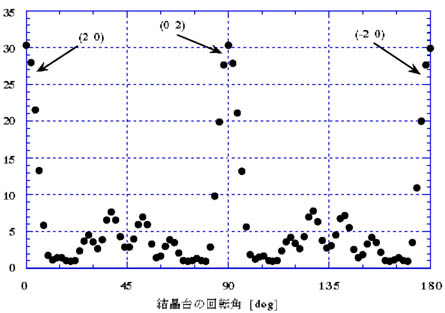
図29 二次元直交格子からの散乱(格子定数a=b=6[cm]、波長λ=3.27[cm])
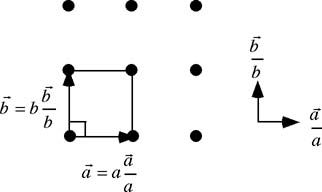
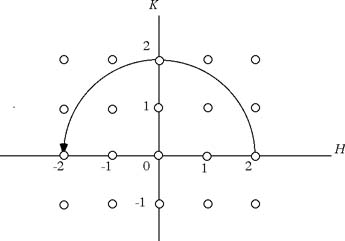
図30 直行格子のunitcell
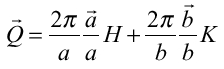
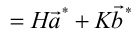
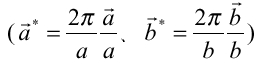
実験6_1
図20の様に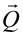 を変化させ、K=0としてHを1.6から3.5まで0.1ごとに変化させて(H 0)Scanを行え。
を変化させ、K=0としてHを1.6から3.5まで0.1ごとに変化させて(H 0)Scanを行え。実験6_2
図21の様に を変化させ、K=2としてHを0から2.9まで0.1ごとに変化させて(H 2)Scanを行え。
を変化させ、K=2としてHを0から2.9まで0.1ごとに変化させて(H 2)Scanを行え。設定は次の通り。
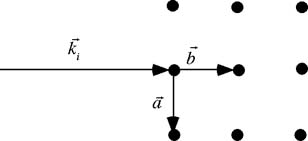
図31 初期設定
図31の様に原子棒を配置し(a=b=6[cm]、三本三列)、入射ビームと格子の
 方向を同一にして、その後Labviewに従って結晶台をω、受光器をψだけ回転させよ。
方向を同一にして、その後Labviewに従って結晶台をω、受光器をψだけ回転させよ。
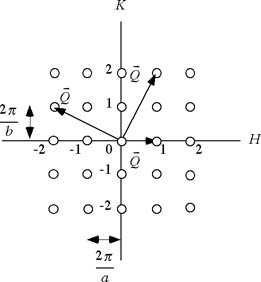
 方向にも周期性をもたせたらどうか。二次元直交格子からの散乱を考えよう。
方向にも周期性をもたせたらどうか。二次元直交格子からの散乱を考えよう。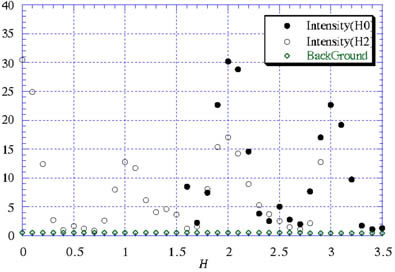
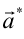 方向に周期性がなかったため、Hの値によらず位相差が0(実験5_1)、4π(実験5_2)で強め合っていたが、二次元では
方向に周期性がなかったため、Hの値によらず位相差が0(実験5_1)、4π(実験5_2)で強め合っていたが、二次元では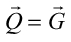
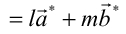
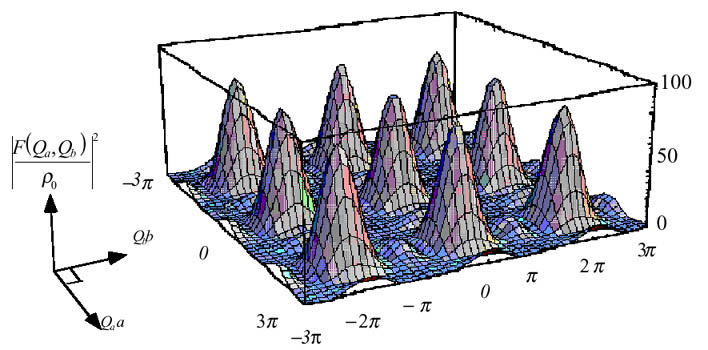
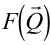 の絶対値の自乗を表している。ここでもIntensityは
の絶対値の自乗を表している。ここでもIntensityは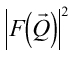 に比例している。
に比例している。