実験8
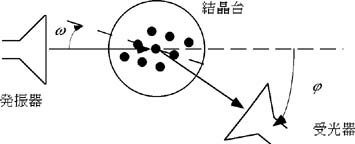
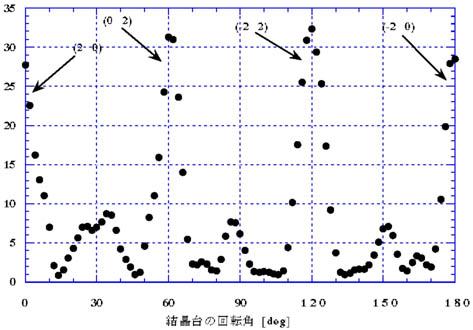
図37 二次元三角格子からの散乱(格子定数a=b=4.5[cm]、波長λ=3.27[cm]
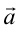 方向と
方向と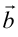 方向のなす角γ=120°)
方向のなす角γ=120°)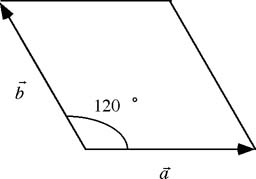
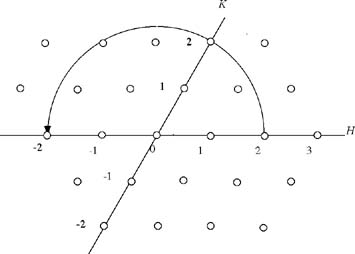
図38 実格子unitcell
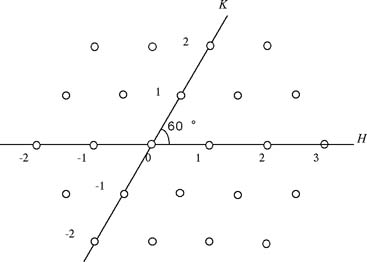
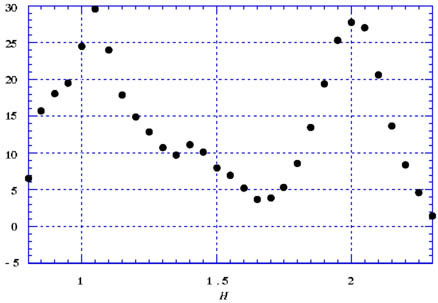
逆格子空間と逆格子点を描きなさい。また、図37の様に原子棒を配置し(a=b=4.5[cm]、γ=120°、三本三列)、K=0としてHを0.8から2.3まで0.05ごとに変化させて(H 0)Scanを行え。設定は実験6と同様にせよ。
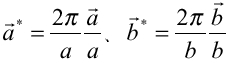 と記述したが、実はこれは
と記述したが、実はこれは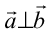 の時にのみ成立するものであって、一般的な表現としては正しくない。
の時にのみ成立するものであって、一般的な表現としては正しくない。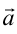 、
、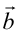 、
、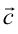 が結晶格子の基本並進ベクトルであるとき、その逆格子の基本並進ベクトルは、
が結晶格子の基本並進ベクトルであるとき、その逆格子の基本並進ベクトルは、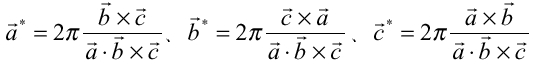
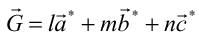 (l、m、nは整数)
(l、m、nは整数)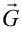 を逆格子ベクトルという。
を逆格子ベクトルという。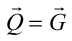
実験8
図37 二次元三角格子からの散乱(格子定数a=b=4.5[cm]、波長λ=3.27[cm] 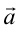 方向と 方向と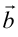 方向のなす角γ=120°) 方向のなす角γ=120°)
図38 実格子unitcell 逆格子空間と逆格子点を描きなさい。また、図37の様に原子棒を配置し(a=b=4.5[cm]、γ=120°、三本三列)、K=0としてHを0.8から2.3まで0.05ごとに変化させて(H 0)Scanを行え。設定は実験6と同様にせよ。 |

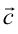 はab平面に垂直な方向の単位ベクトル)
はab平面に垂直な方向の単位ベクトル)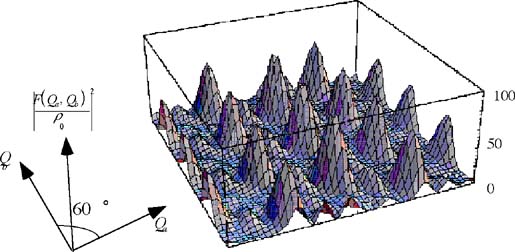
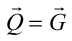
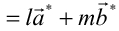 (l、mは整数)
(l、mは整数)
実験9実験8のときの(2 0)の位置にω、ψを合わせ(ω=57.04°、ψ=114.09°)、ψを固定したままωをその位置から2°づつ、180°回転してIntensityを測定せよ。 |