強磁性体と反強磁性体の基本的な性質について簡単に説明する。
そのためにここでは２次元イジングモデルにおけるモンテカルロシュミレーションにより得られる結果
を利用するが、より詳しい説明は３Ｂ実験（磁性体のモンテカルロシュミレーション）の中で用意されている。
ゼロ磁場の元での強磁性体と反強磁性体の２次元イジングモデルのハミルトニアンHは
で表せる。
ここで、
は
と
の間の交換相互作用、とは磁気モーメントである。
シュミレーションはfig.1.1に示す様な最近接相互作用のみ、そして磁気モーメントＳ＝±１の元でおこなった。
強磁性体と反強磁性体の磁化Ｍと帯磁率χの温度依存性は以下のような結果 となる。
fig1.2強磁性体と反強磁性体の振る舞い
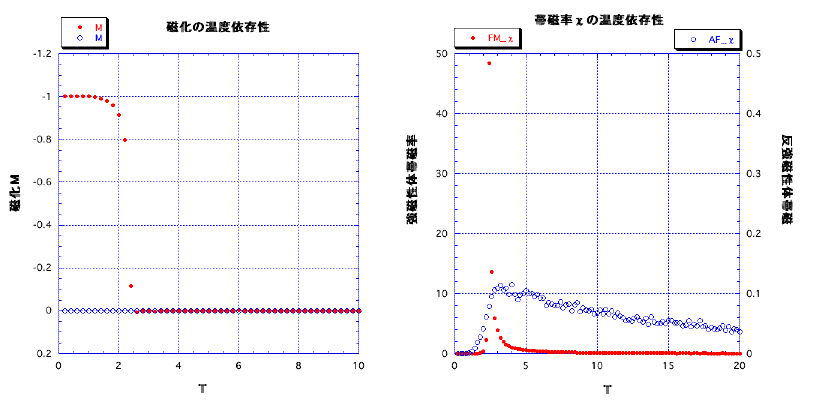
磁化の増加や帯磁率のピークから、強磁性体はT≒2.3において相転移していることが確認される。 この結果はOnsagerの厳密解より転移点の温度Tc が
と求められることを反映している。 一方、反強磁性体の磁化に変化はなく相転移した様子は読みとれない。これはこのシミュレーションで観測している磁化というのは、全スピンの平均値である一様磁化であり、反強磁性体のように反平行に並んだスピンにおいては、一様磁化は相殺されゼロになるからである。
また反強磁性体の帯磁率はTcより高い温度でブロードなピークを示すだけでTcでは発散しない。
しかし実際に反強磁性体のspin mapの温度変化をみると、反強磁性体にもはっきりとした相転移が確認される(fig.1.5)。これは一様磁化や一様帯磁率は相転移の様子を見て取るのに適した物理量
ではないということを示している。 そこでスピンの平均値をみるのではなく、空間的に一様でない秩序についても言及できる一般
化磁化 
という物理量
を導入する。