1.3 ![]() の説明
の説明
が表すものについて説明していくが、ここではこれから利用する概念を天下り的に紹介してまとめ、詳しい内容については「よくわかる2次元正方格子(1996 根本)」、「一次元イジング磁性体における空間相関(1997 宮本)」、「2次元正方格子Ising spin model磁性体の希釈効果とランダム磁場効果についてのMonteCarlo Simulation(1997 井ノ川)」に譲る。
先に示した2次元のを対角線方向に一次元にカットした断面 に当たるグラフをspin mapと並べて示し、その
のグラフのいくつかの温度について 抜き出したグラフを使って説明を加える。
なお対角線方向とは(h,h)方向にあたり、M(0,0)=M(0)、M(1/2,1/2)=M(1/2)にあたる。fig.1.7 spin mapと
強磁性体
反強磁性体
反強磁性体の
を例にとるとfig.1.8に示す情報を読みとることができる。もちろん 強磁性体についても長距離秩序があらわれる波数が違うだけで同じ様に読みとることができる。
fig.1.8
の示すもの
帯磁率とは磁化のゆらぎであり次式の関係をもつ
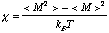
一般化帯磁率χ(Q)について言えば
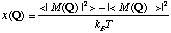
と表されるのでは
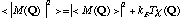
である。
このことからが、系全体にわたる秩序である長距離秩序をあらわす量
とゆらぎをあらわす量
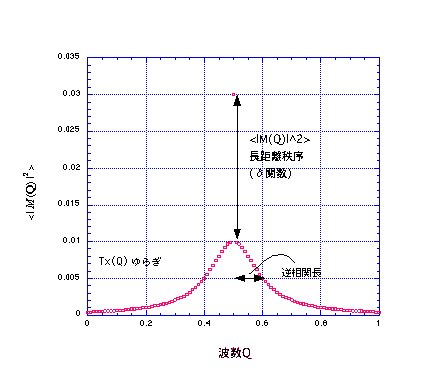
の和であることがわかる。先に示したfig.1.5のグラフにおいて、注目していた逆格子点のまわりが盛り上がっていたのはこの
のためである。
の温度変化を観察すると相転移点Tcより高温では長距離秩序はなく、そのため
となり十分高温では波数Qによらず
はほぼ一定値をとる。これは高温では常磁性相にあり、状態が均一に拡散していることを示している。 また温度を下げていくと相転移点Tc以下でδ関数型の長距離秩序が現れ、その波数のまわりでゆらぎが生じている。
さらにという物理量 からは逆相関長というゆらぎの指標となる長さを観察することができる。これは図示したように
のみの関数のピーク(fig.1.8では
=0.01)の半分の値の
の幅を半分にした長さである。(半値半幅、HWHM )
は逆空間の関数であるから逆相関長は[1/長さ]の次元を持ち、逆相関長の逆数である相関長は[長さ]の次元をもつ。逆相関長や相関長は、離れたサイトにあるスピン同士の関係の程度、つまり相関を示す。相関長が長ければあるスピンの動きが離れたサイトにあるスピンにも影響をあたえ、短ければ影響しにくい。
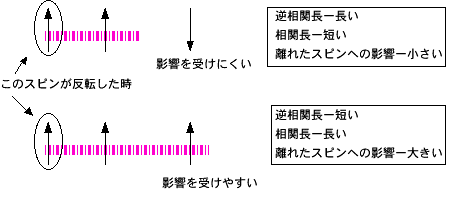
fig.1.9 逆相関長と相関長2次元のspin mapについて考えれば、相関長が短い時は同じ秩序をもった区間の範囲は狭く細かい区間に分断されて、お互いの影響は小さい。しかし相関長が長くなると同じ秩序をもった区間が広がり長距離秩序を形成する。
その様子をいくつかの典型的な温度についてとspin mapを抜き出して説明する。ここでは高温から低温に変化させた様子を順に並べてある。
相転移点Tc以上の温度では、強磁性体と反強磁性体ともに常磁性相にあり、状態が均一に拡散している。この時
は波数によらず一定値をもつ。
Tc=2.27付近ではゆらぎが大きくなり、逆相関長が徐々に短くなる。つまり相関長が伸び、同じ秩序の区間が広がりはじめる。そしてこの (B)T=2.6ではまだ長距離秩序はあらわれていない。
T=2.2では長距離秩序があらわれており、それがspin mapからも
からも読みとれる。(注;この
グラフの縦軸は対数である)またゆらぎは(B)T=2.6とくらべて小さくなっている。
Tc以下ではゆらぎは減少しT=0.4ではほとんどなくなり、値をもつのは長距離秩序のみとなる。
それでは温度を下げていく過程の強磁性体と反強磁性体の逆相関長κを
に次式をfittingさせることにより求めてみる。
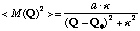
(aはピークの頂点,はピークの波数)
fig.1.11 強磁性体と反強磁性体の逆相関長
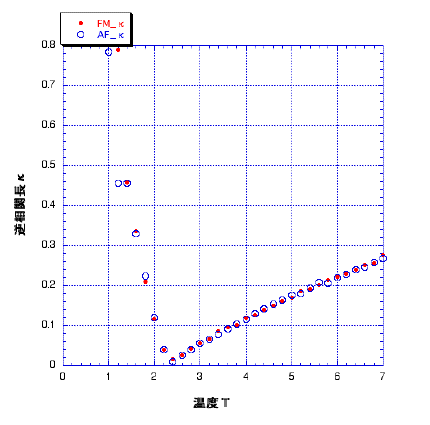
強磁性体と反強磁性体の逆相関長は等しく推移する。これは相転移がおこっている間のゆらぎの大きさが等しいということであり、磁化、帯磁率でみられた 強磁性体と反強磁性体におけるdualityが、相関長の温度変化にも見られることになる。ここに空間相関をもちいて相転移現象を確認する価値があると言える。
また逆相関長κは転移点Tc=2.4まで減少していく、つまり相関長が伸びていく。これはある秩序(この場合、反強磁性的なup-down-up-downの秩序)が広がっている様子とゆらぎが増えてゆく様子を示している。またTc=2.4を越えたところでκが増えるのは長距離秩序が現れ平均からのずれが顕著になるからである。このように多くの有用な情報を含む
のグラフを用いて、次章からフェリ磁性体の説明をしていきたいと思う。