Waves and Oscillation
Produced by Mitsuda Lab.
Session4 連成振動 (Two-Coordinate Vibration)
1 はじめに
ここまで自由度=1の調和振動子の運動を調べてきたが、複数の調和振動子が結合した力学系を考えよう。
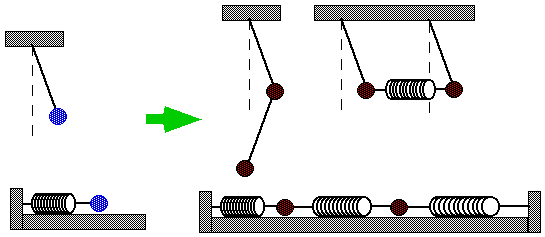
複数の調和振動子が結合した力学系は、一見すると調和振動子とかけ離れた複雑な運動を示すように思えるが、意外にも、「基準振動」(Normal Modes)と呼ばれる複数の独立な調和振動の重ね合わせで表現できることを、ここでは学ぶ。
2 Normal Modes ?
バネで結ばれた2個の調和振動子 (Movie)の例題を通して「基準振動」(Normal Modes) および「基準座標(Normal Coordinates)」について学ぶ。
3 How to find the normal coordinates
「バネで結ばれた2個の調和振動子」の例ではバネ定数&質量に関して左右の対称性が高いために、連立微分方程式の和と差を取ることにより簡単に基準振動を見つけることができたが、以下の例「バネで結ばれた重さの異なる2個の調和振動子」や「二重振り子」の様な場合、「基準振動」を系統的に見つけるにはどうしたらよいのだろうか?
ここでは、運動エネルギーとポテンシャルエネルギーの2次形式の対角化による方法を学ぶ。
「バネで結ばれた重さの異なる2個の調和振動子」ではスケール座標変換に続く回転座標変換により質量が1に、バネ定数が対角化されたポテンシャルエネルギー行列の固有値になっていることを、対照的に、「二重振り子」ではスケール座標変換に続く回転座標変換によりバネ定数が1に、質量が対角化された運動エネルギー行列の固有値になっていることを学ぶ。
バネで結ばれた重さの異なる2個の調和振動子 (Movie)
二重振り子 (Movie)
