第４集　アンペールの法則

～クイズを答えてアンペールの法則を理解しよう～

　第３集『静磁場の性質』で、「直線電流のまわりには直線電流に対して軸対称な磁場ができること」を学びました。具体的には、直線電流から距離ρだけ離れた点の磁場は、１／ ρに比例します。

　これから様々な場面で磁場の値を計算していく時に、ビオ－サバールの法則で計算するよりも楽な方法があります。それが『アンペールの周回積分の法則』と呼ばれるものです。
　その内容は、「定常電流Ｉが作る磁場を任意の閉回路Ｃについて周回積分した値は電流値Ｉのみに依存する」というもので、磁束密度大きさをＢとすれば任意の閉回路Ｃについて

と表すことができます。

　ここでアンペールの法則を体感するために、左の装置を使います。これは、「Rogowskiスパイラル」と言って直径約２cm、長さ１mほどのゴム管にコイルを約1000ターン巻いた検出コイルです。

【実験の下準備】

「この装置の役割は？」

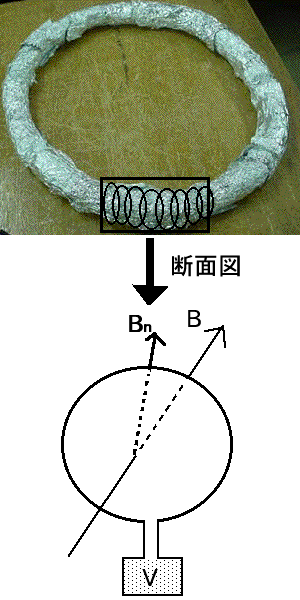
　この疑問を解決するために、ゴム管にコイルを巻きつけたことによってできた環（わ）のうち、※一つの環に注目して考えてみましょう。

※（以下『コイルＡ』と呼ぶことにします）

　コイルＡの面に垂直な磁場成分をＢnとします。実験では※交流を扱っているので、時間とともに変位する磁場が生じます。よって、このコイルには誘導起電力Ｖが現れます。
　※そもそもアンペールの法則は定常電流についてのみ成り立つ法則であり、交流電流には本来適用することができません。しかしこの実験では、「準定常電流」と呼ばれる低周波の交流電流を扱っているのでアンペールの法則を体感するにあたって大きな影響を与えません。このことについては後ほど詳しく記述します。

　ひとつの環について得られた誘導起電力を全て足し合わせたもの（Ｖ１＋Ｖ２＋Ｖ３＋Ｖ４＋…）は結局、直線電流がつくり出す磁場のうち、Rogowskiスパイラルに沿った磁場成分（赤の矢印で示したもの）からくる起電力の和となり、式で表せば

とほぼ同値であることがわかります。

　これからこのRogowskiスパイラルを使って、アンペールの法則を体感する実験をいくつか行います。すべての実験においてオシロスコープに表示された値Ｖは、

であることを頭において、問題を考えてみましょう。