PHYSICAL GRAFFITI

BBS

mail

link

■トップ > 固体物理 > ２次元逆空間の構造因子

２次元逆空間と構造因子

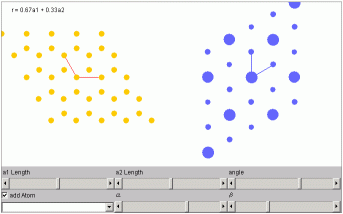
現在製作途中。左側が実空間、右側が逆空間です。
ここではブラッグ散乱強度は構造因子の大きさによってのみ定まるとして、逆格子点の大きさはその点に対応するブラッグ散乱強度を示している。「Add Atom」をチェックすると、単位格子内に原子が１つ追加され、その位置はスクロールバーで変えることができる。

　実空間での基底の角度を１２０度にして、「ａｄｄ　Ａｔｏｍ」をチェックし、 α＝２／３（＝０．６７）、β＝１／３（＝０．３３）とすると、実空間では六角形の蜂の巣格子ができる。　逆空間では（１，１）方向に他と比べて２倍強い反射が現れる。左下のチョイスでミラーナンバーを指定すると、面が表示できる。
　α＝１／２（＝０．５）、β＝１／２（＝０．５）とすると、（１，０）（０，１）方向の反射強度がゼロになる。
　反射面を見ると、緑の線で表示された面のちょうど中間に、加えられた原子による面ができていて、半波長分ずれた波が反射されることになる。よって回折線は現れない。

構造因子

　単位格子が原子を複数個含むとしたときには、面の指数によって散乱強度が変わってくる。それを示す量が構造因子であり下の形で与えたれる。

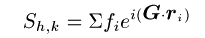
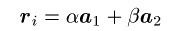
　ここでｒiは考えている単位格子内での原子の位置を基底ベクトルで現したものである。ｆiは「原子形状因子」または「原子散乱因子」といい、その名の通り原子の形状による散乱の度合いを表す量である。いま全ての原子は同じ種類のものとするので、以下定数とする。

このアプレットの場合は単位格子に２つの原子を含んでおり、一つは上の式で与えられる点にあり、もう１つはα＝０、β＝０の点にある。
　逆格子ベクトルは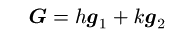

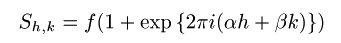
であるから、上のアプレットで考えている２次元の系の（ｈ、ｋ）面の構造因子は

となる。α＝β＝１／２　とすると、「ｈ＋ｋ＝奇数」のときに構造因子はゼロとなり、反射が見られなくなる。
また、見て分かるように、構造因子は複素数である。散乱強度は|S|^2で与えられる。