組合せデザインって？

「3人組で対戦するゲーム(ダイヤモンドゲームなど)を7人で遊びたい． 皆が公平に対戦できる(自分以外の人とは必ず1回ずつ対戦し, 各人は3回のゲームを行う)ような組合せを考えなさい．」というような問題は, 離散数学の分野で組合せデザインと呼ばれています． では，どのように構成できるのでしょうか?

有限射影平面と組合せデザイン

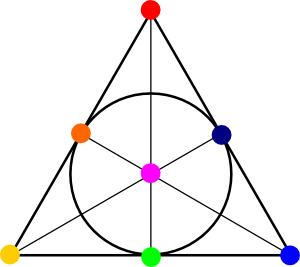7人を左の図の各頂点にとり，対戦する組を直線と考えてみましょう． 各頂点はちょうど3本の直線に含まれていることがわかります，このような 組合せ構造は位数が2の射影平面と呼ばれています． ちょうど上の問題の答えになっていますね！

代数系と組合せデザイン

では次に7人の人を0から6までの数字で表現してみましょう． このとき対戦する組をブロックと呼び，各ブロックの要素が対戦するメンバーとなります． 右の B1, ... B7 がブロックの集合で，B1の各要素に1ずつ加えると， 他のブロックが巡回的に表現出来ます．少し難しくなりますが， B1の2つの要素の差を考えてみると法7のもとで0から6までの全ての数字が 1回ずつ出現するという，差集合と呼ばれる代数的性質を持っていることがわかります．

パズルと組合せデザイン

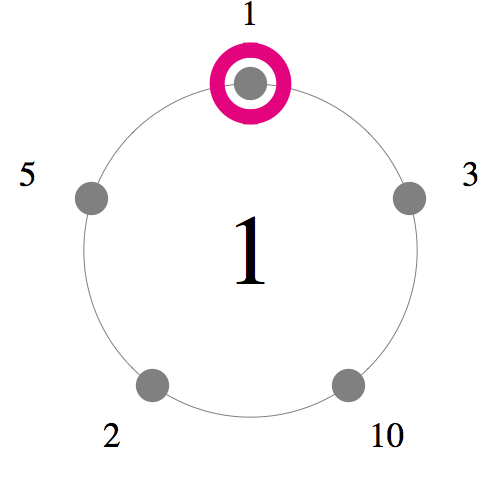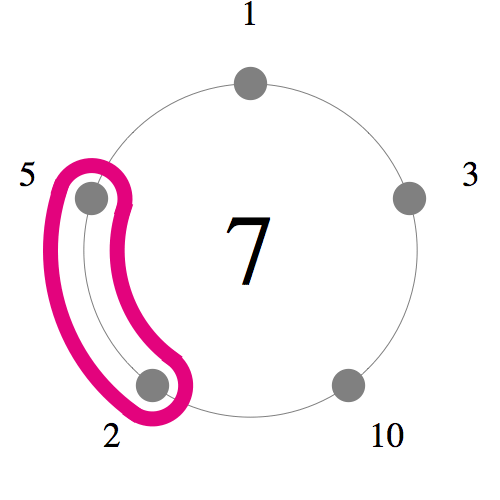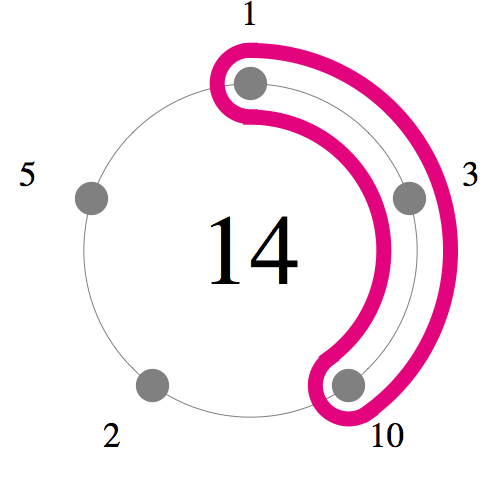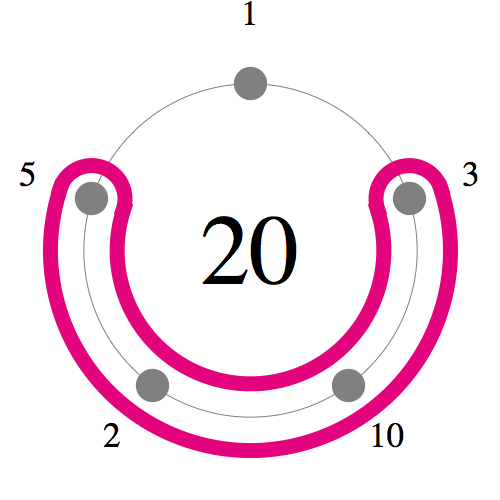図のように5つの数字を円に並べます。いろいろな弧の選び方がありますが、 その弧に現れる数字を足してみると, 1から20までの数字がちょうど1回ずつ現れます。 これは魔円陣などと呼ばれています。 こんな数字の並べ方を、他にも見つけられるでしょうか？ ラテン方陣や魔方陣など、パズルのようなものを深く追求すると、 組合せデザインの考え方にいたることがあります。 実は魔円陣は、本質的には差集合と同じものなのです。

実験計画法と組合せデザイン

実験計画法は実験によってデータを獲得する前の計画のための統計的手法です． 例えば，農業実験で小麦の7種の品種の収量を比較したいとしましょう． 広大な農地に適当に植えて，収量を測るのでは， 日照条件や土壌条件が揃わず正確な判断が下せません． そこで農地を7つのブロックに分け，さらに書くブロックを 3つのブロックに分けて品種を作付けします． この割り付け方に上記のブロックを用います． 各ブロックごとに環境条件が均一になるように管理すると， 品種の効果をより精度を高く推定することが出来ます．