研究紹介
これまでの研究テーマ
過去の卒業論文、修士論文、博士論文で行われた研究テーマはこちらをご覧ください。
マクロスケール解析
材料の特性を知るためには、様々な状況下で実験を行う必要がありますが、膨大な時間とコストがかかります。そのため、数値解析を用いた材料シミュレーションが注目されています。本研究室では、マクロスケールでの材料シミュレーションの手法の1つである有限要素解析 (FEM: Finite Element Method) を用いた材料の強度解析を行っています。
切り欠き付き配管の延性破壊に関する有限要素解析
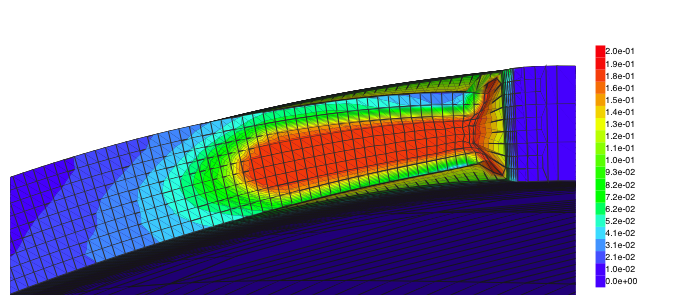
初期の設計寿命を超える軽水炉プラントの運転継続のためには、欠陥が検出された場合の運転継続の可否を決定する「欠陥評価法」の整備が必要です。現行の欠陥評価基準はクラス1と呼ばれる高靭性の配管が対象であり、クラス2・3と呼ばれる中靭性の配管に対しては、検出された欠陥に対する評価方法は設定されていません。そこで本研究室では、代表的な中靭性配管材であるSTPT410炭素鋼に対して、ボイドと呼ばれる空孔を考慮したGursonの降伏関数を有限要素解析に取り入れ、切欠き付き配管の4点曲げ試験のき裂進展解析を行っています。
有限要素法による疲労き裂進展解析
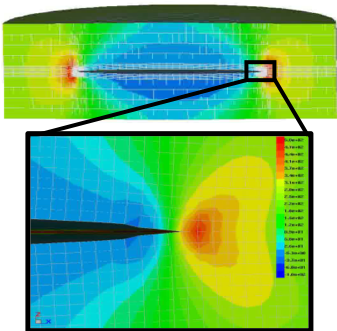
構造物・機器の事故の1つに、繰り返し荷重によるき裂成長があります。近年では、多くの産業機械や構造物が繰り返し荷重を受ける環境下にあるため、疲労き裂進展挙動と余寿命評価の予測を行うことは重要です。一般に、疲労に関する実験を行うことは多くの時間や費用がかかります。そこで本研究室では、有限要素法による数値解析を行い、疲労評価、き裂進展挙動の確認・評価を行っています。中でも重合メッシュ法や結合力モデルを用いた疲労き裂進展解析により、計算コストの削減や複雑なき裂の様々な条件での解析が可能になります。
メゾスケール解析
多くの産業機械や構造物には金属材料が使われています。一般に金属材料の変形は、弾性変形と塑性変形の2つに大別できます。弾性変形では与えられた荷重を取り去った後に元の形状に戻りますが、塑性変形では与えられた荷重を取り去っても変形がほとんど戻ることはありません。金属材料の塑性変形は、材料中に存在する線状の欠陥である転位の移動によって起こります。そのため、金属材料の変形の本質を理解するためには、転位の挙動を詳細に理解することは必要不可欠です。本研究では、転位動力学法 (DD: Dislocation Dynamics) を用いた転位挙動の解析を行っています。
転位—析出物相互作用シミュレーション
不純物原子や析出物などの母相と異なる第2相粒子を利用した金属材料の強化法として、析出強化、分散強化、固溶強化などの強化機構が一般に知られています。これらの強化機構では、金属材料中の第2相粒子が転位の運動に対する障害となりることで、臨界分解せん断応力 (CRSS: Critical Resolved Shear Stress) が上昇すると考えられています。
析出物と転位挙動の関係は、強化機構によって異なります。析出強化では、母相と析出物の格子定数の違い(整合ひずみ)が弾性ひずみ場を生成し、転位の運動に影響を与えます。しかし、析出物は微細なため、転位は析出物をカッティングしながら進んでいきます。分散強化は、母相よりも硬く塑性変形しにくい粒子が転位の運動の強い障害物なることで材料を強化する手法です。この手法では、転位は粒子を迂回して進み、粒子のまわりに転位ループを残すオロワン機構と呼ばれる現象が見られます。析出強化においても、粒子が大きくなり転位が粒子をカッティングできなくなるとオロワン機構に遷移します。そのため、析出強化は分散強化と本質的に変わらないと考えられています。
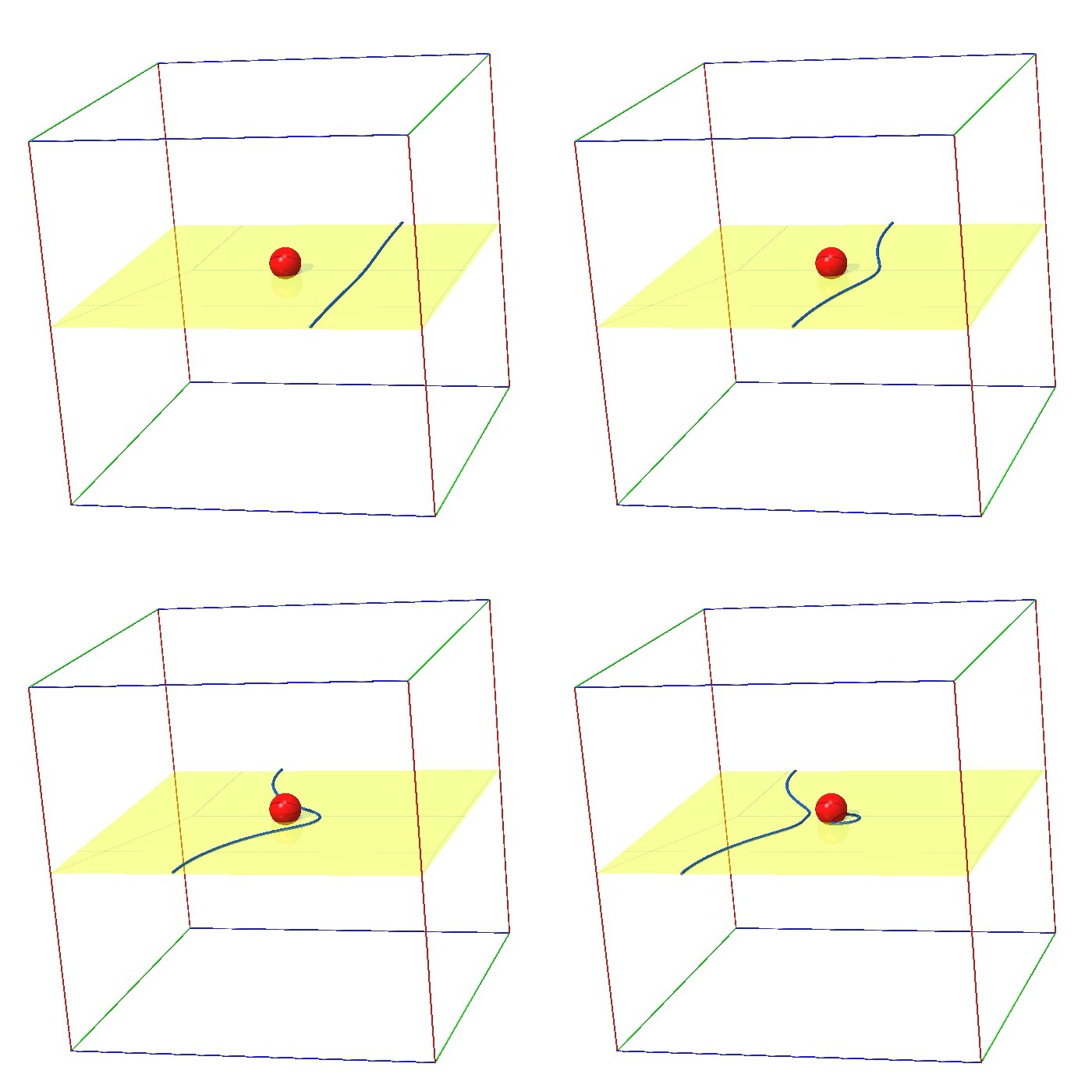
実際の材料では様々な機構が混在しているため、析出物のみの影響を実験的に調べることは困難です。そのため、析出強化のカッティング機構から分散強化のオロワン機構への遷移メカニズムは解明されていません。そこで本研究室では、転位と析出物の相互作用を考慮したシミュレーションを行い、遷移過程を明らかにしています。図は、整合ひずみが生じている場において、1本の転位が析出物に接近し、オロワンループを形成した後に析出物から抜けていく様子を表しています。
転位の近距離相互作用シミュレーション
転位の近距離相互作用にジョグとジャンクションが挙げられます。ジョグは転位同士の切り合い、ジャンクションは転位同士の合体を表しています。本研究では、これらの転位の近距離相互作用を再現した転位動力学シミュレーションを行っています。図は近距離相互作用シミュレーションを可視化した一例です。青い線は転位を示しており、水色の点でジョグを、黄色い線でジャンクションを表しています。ジョグやジャンクションなどにより、転位同士が複雑に絡み合っている様子が再現できていることが分かります。

ミクロスケール解析
金属材料をはじめとするすべての材料は、数多くの原子が集まって構成されています。材料の強度問題や材料中の転位挙動はこうした原子スケールでの現象に起因していることがあります。そのため、原子スケールでこれらの解析を行うことは不可欠です。本研究では、古典分子動力学法 (MD: Molecular Dynamics method) を用いることで、材料の強度や転位を原子スケールで明らかにしています。古典分子動力学法とは、多数の原子に対し古典力学に基づくニュートン運動方程式を適用することで原子の運動をシミュレーションする手法です。この手法では量子効果を取り入れた計算を行っていないため、第一原理計算よりも大きな空間・時間スケールでの解析が可能です。
NEB法を用いたBCC鉄中の熱活性化運動による活性化エネルギーの算出
BCC鉄におけるキンク対形成の活性化エネルギーをNudged Elastic Band (NEB) 法を用いて算出しています。 これにより,さまざまな形状の転位のパイエルス応力が算出できました。また、この結果により、キンク対形成の活性化エネルギーの転位線方向に沿った原子間距離に対する依存性や、適用されたせん断応力に対する活性化エネルギーの依存性も解明されました。現在は、混合転位移動との関係性について解析を行っています。

ナノインデンテーションにおける結晶方位依存性の分子動力学
材料における引っ張り強さや割れ耐性といった材料特性は設計製作において重要な要素です。これらの材料特性と一定の関係を持つ硬さを算出するために用いられる材料試験が、ナノインデンテーション試験です。本研究では、分子動力学法を用いたナノインデンテーションの数値シミュレーションを行い、実験で明らかになった硬さの結晶方位依存性のメカニズムを明らかにしています。



