数理モデリング研究部門

研究会の開催

• 神楽坂解析セミナーの開催（年７回程度）
• 数理物理学講義の開催（年１〜２回）
• 神楽坂「感染症にまつわる数理」勉強会の開催（年４〜５回）
• 野田キャンパスでの研究会の共催（談話会）
• 「解析学とその周辺」＠野田

主な研究テーマ

1. シュレディンガー方程式の解の表現を用いた数値計算
2. 偏微分方程式の逆問題の他分野への応用
3. 感染症の数理モデルの理論的研究，数値シミュレーション

シュレディンガー方程式の解の表現を用いた数値計算

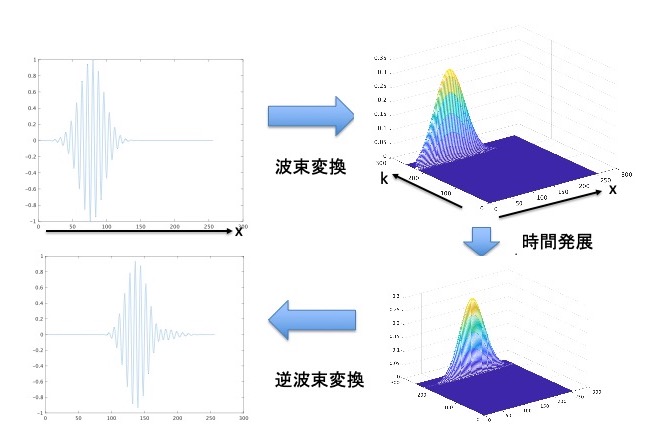
シュレーディンガー方程式などの方程式の解の新しい数値解法を完成し，開発した数値解法を具体的な問題に応用することを目的としています。 加藤らが開発した波束変換を用いたシュレディンガー方程式の解の表現公式を物性物理学に応用することを模索しています。波束変換を用いたシュレーディンガー方程式の解の表現方法の数値計算に適する改良に成功し，実際に数値計算を試みています。また，数理物理学に関連する講演会や連続講義を企画しています。

偏微分方程式の逆問題の他分野への応用

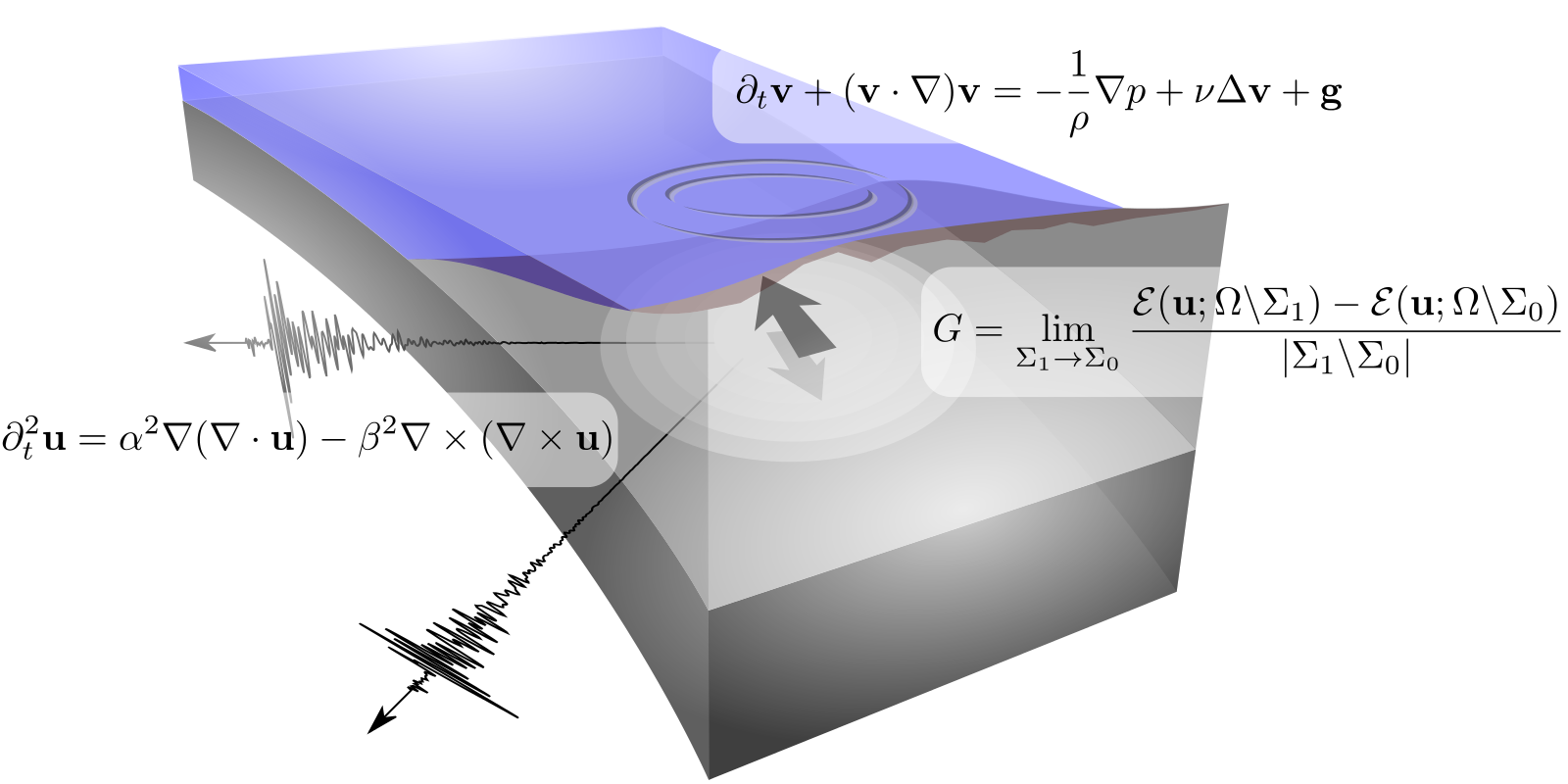
弾性構造物における破壊現象や流体現象（渦糸の運動）などの数学解析を行うと共に、地震時における断層破壊や逆問題への応用について考察します。逆問題については生体における非侵襲的な検査や材料における非破壊検査に由来する媒質中に潜む不連続性（空洞、き裂、介在物や障害物など）の位置や形状の情報を観測データから抽出する再構成の問題や、地震学における震源過程の逆解析を考察することが目的です。また、海外からの専門家の招聘やセミナー・国際研究集会の開催を行っています。

感染症の数理モデルの理論的研究，数値シミュレーション

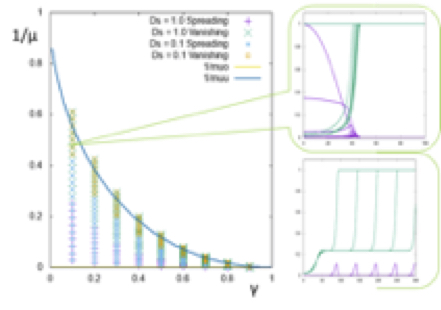
感染症流行を記述する感染症モデルや癌の浸潤現象等を記述する走化性モデルをはじめとする、時間発展に伴う生物個体数の増減を調べるための数理生物モデルの解の漸近挙動の解析を行っています。本研究グループの石渡恵美子、牛島健夫、江夏洋一による感染個体の生息領域の拡大を記述した自由境界問題に関わる共同研究では、個体の出生や死亡を考慮しない短期流行モデルにおいて、形状を保ったまま空間上を伝播するような進行波解の存在・非存在に関する新たな結果が得られています。

また、2018年2月より、神楽坂「感染症にまつわる数理」勉強会を開いています。感染症に関連する研究を行う数学・生物学・医学などの幅広い分野の研究者から、感染症にまつわる話題を定期的に提供していただいています。