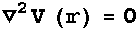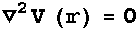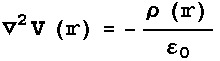2 Electrostatics (静電気学)

●Chapter2とChapter3では種々の電荷分布がどのような場をつくっているか、を求めることが中心となっています。
一年生の学生実験で体感した次の題目も思い出しながら進んでください。
・クーロンの法則《01年度卒研生三島央さん作成》
・静電場の性質《01年度卒研生三島央さん作成》

具体的に電荷分布がどのような静電場をつくっているかを求めるには、以下の４つの方法があります。このChapter2では《方法1》～《方法3》について学び、《方法4》については、次の Chapter3:Special Techniquesで見ていきます。

《方法1》電荷のつくる電場をベクトル的に加える(積分する)方法（TEXT pp.60-64）
　　　　　→例:円盤のつくる電場と電位（Prob. 2.6 TEXT p.64）

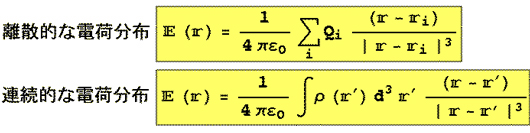
《方法2》電荷がつくるポテンシャルを加算(積分)し、そのgradientを計算する方法（TEXT pp.77-87）

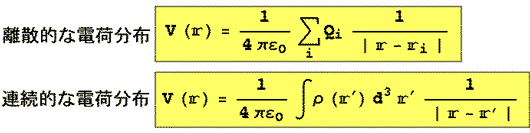
《方法3》Gauss's Law(ガウスの法則)を用いる方法-対称的な電荷分布の場合（TEXT pp.65-76）

《方法4》ポテンシャル（電位）に関する場の方程式である
Laplace's方程式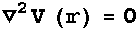　　

　　Poisson's方程式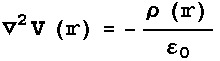　　

を解く方法（TEXT Chapter3:pp.110-）

様々な電荷分布の場合に、このようにして求められた電場や電位がどのようになっているかを確認するには以下をクリックしてください。
・点電荷
・線電荷分布
・面電荷分布
・球殻電荷分布
・球電荷分布

・有限長の線電荷のつくる電場と電位
・円盤のつくる電場と電位

詳しくはChapter3で触れることになる、電気双極子(Electric Dipole)と電気四重極子(Electric Quadrupole)については、次を参照してください。
・電気双極子(Electric Dipole)
・電気四重極子(Electric Quadrupole)

電気力線や場については、次を参照してください。
・電気力線の幾何学的性質
《小泉修さん（1201039）の作品》点電荷による電場ー点電荷を自由に配置し、そのベクトル場を描くアプレット

電場に蓄えられたエネルギー
・点電荷分布に蓄えられたエネルギー（QuickTime Movie:順次クリックして見てください）

・点電荷分布に蓄えられたエネルギー（PDFファイル）