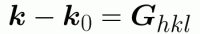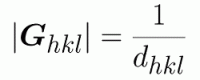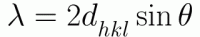■ 単結晶によるX線回折〜Laue Method〜
|
目的: X線の発生および結晶による回折機構を理解し、これに基づいてラウエ法を用いて単結晶の結晶方位の決定法を学ぶ。 ・実験課題 白色X線を試料(Mo単結晶)に照射し、反射X線をポラロイドフィルムに記録する。 得られた干渉図形の斑点の指数付けを行い、その試料表面のミラー指数を決定する。
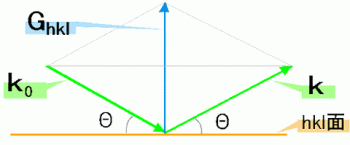
「逆格子ベクトル」を用いると、結晶中の平行な原子面の組をまとめて表すことができる。逆格子ベクトルの基底定義は下のようなもの(およびその循環式)で、 それぞれに整数の組(h、k、l)をかけたベクトルGはある原子面に垂直なベクトルである。 よってある平行な原子面軍は、まとめて「hkl面」と呼ぶ事ができる。 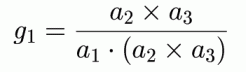
<<構造因子>> これらの散乱条件式は回折線が現れる位置のみを予測する。しかしこれだけでは実験とは合わない。 「構造因子」というものを考慮すると、体心立方格子ではh、k、lの和が偶数になるときのみ回折線が現れる事が分かる。 |