■ 単結晶によるX線回折〜Laue Method〜
|
<<構造因子 (Structure Factor) とは?>> 構造因子は、その結晶の本来の基底(Base)ベクトルではないベクトルで結晶を記述するときに用いる。 本来の基底ベクトル(a1,a2,a3)は、各ベクトルの整数倍によって結晶内の全ての原子の中心を指し示す事ができる。 また、基底ベクトルを3辺に持つ平行六面体を「基本単位格子(Primitive cell)」といい、1つの原子を含む。 しかし、体心立方格子や面心立方格子などの基底は対称性が高くない。 そこで、対称性の高い基本並進ベクトルと、それがもとの結晶の情報を再現するように「構造因子」を用いる。 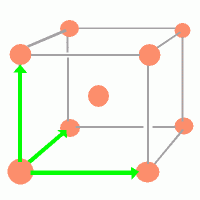
今回の実験の場合Moは体心立方格子なので、この格子について考える。 上記のアプレットで見ても分かるように、 体心立方格子の基底はひし形の面を持つ平行六面体である。しかし、その基底に代えて右図のような基底を導入する。 このベクトルは、並進対称性を満たしているが、図の中央の原子は、各ベクトルを0.5倍したものの和であらわされる。 (整数倍でない)。なおかつ、右図の立方体は原子を2個含むのでこれも基本単位格子(Primitive Cell)ではない。 しかし右図緑のベクトルは対称性が高いし、逆格子ベクトルを求めるのも容易なので(逆格子ベクトルと方向が同じ)、 これを用いて回折を記述する事にしたい。しかしこのままだと体心立方格子ではなく単純立方格子になってしまうので これに見合った「構造因子」を用いる。 本来の基底でない並進ベクトルを用いて、作られる逆格子ベクトル群があり、それらは回折スポットに対応するが、 その斑点の明るさ(反射光の強度)は構造因子に比例する。 <<構造因子の定義>> hkl面からの反射に関する構造因子は 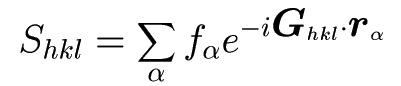
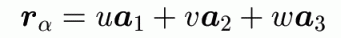
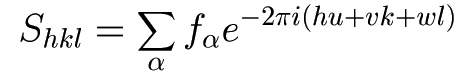
|