採点者(TA)による講評を書き込みます。
AssignmentのLOG(後期)
Assignment#6(後期#1)(10/3)
半径Rの球殻に大きさσ0の一様な表面電荷分布を与えたときのポテンシャルを球殻の内側および外側で求める問題です。答えは自明ですが、ここで問っているのはExample3.9で扱ったと同じく、境界値問題を解くという論法で回答を書くことです。TAの人は論理構成がわかるように書いてあるかどうかだけを大雑把に採点します。授業中にしつこく言いましたが、間違っても3.83式から出発して答えを書くということのないように(そのような場合はゼロ点と採点します)。
---------
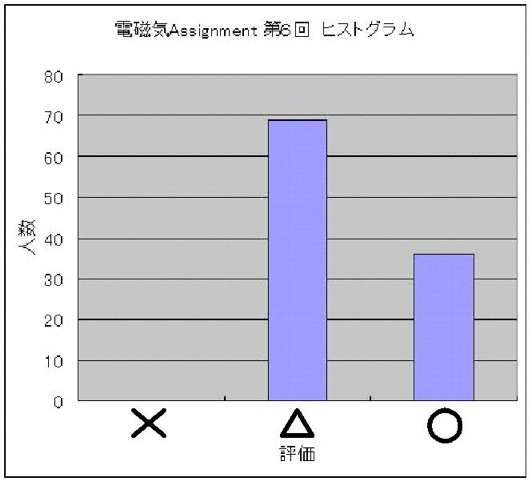
今回は、一様な面電荷密度を持つ球殻の内外のポテンシャルを、境界値問題として解き、グラフを描く問題でした。
採点基準は、
(i)境界値問題を論理的に導けている
(ii)境界値問題を論理的に解いている
(iii)グラフを描いている
で、○、△、×で評価しました。
全体として、解答はほぼ2パターンでした。
・パターン1:教科書Example 3.9の方針にしたがって、まずΘ依存性がある一般的な式(3.84)を導き、その後一様な面密度σ_0(Θ)=P_0(cosΘ)とし、l=0以外で係数がゼロになることを数学的に求めて答えを導くやり方。
・パターン2:まず、Θ依存性がないことを考慮して、Laplace方程式においてr方向以外の微分項がゼロになることから、V(r)=r^pとおき、連続条件からポテンシャルを求めるやり方。
どちらの方法でも同じ解は得られますが、個人的にはパターン2のほうが物理的かな、と思います。
また、どちらのやり方でも共通していえることですが、なぜl=0の項しか残らないのかを明確にしていない人が多く、理解して書いているとは言いがたい解答もいくつか見られました。今回は、曖昧な書き方をしている解答は全て減点しました。
また、計算ばかりに追われて、物理を見失っているひとが多く見受けられました。
この問題自体は別のやり方ですでに解いており、解答を知っているはずですので、得られた解が妥当であるか否かはすぐにわかるはずです。にもかかわらず、二乗がなかったり、Rが抜けていたりといった解答が多くありました。得られた解を吟味する癖を付けてください。
また、l=0ではなく、l=1を考えていた人がいましたが、今回の問題では一様に分布しておりΘ依存性はないので、l=1では間違いです。ここが、Example 3.9と今回の問題との相異点で、キーポイントとなりますのでもう一度よく考えてみてください。
わからなければ質問にきてください。
以上です。 佐藤@TA
---------
Assignment#7(後期#2)(10/17)
半径RのGrounded hollow sphere内に中心点から距離aの場所に点電荷qがある時のPotential問題をmethod of imageにより解く問題を出しました。提出用紙のおもて面に(i) 境界条件を満たす「Image電荷の大きさと位置」を導出するプロセスを論理展開の筋道がわかるように簡潔に書く、(ii) hollow sphereの内壁に誘起される電荷分布σ(θ)の表式を求める、提出用紙の裏面に(iii) 得られた結果をもとに、等電位線、電気力線、内壁に誘起される電荷分布が描かれた図を描く(手書きで十分ですが、等電位線だけならPCでMathematica等を活用すると簡単に描けます)
Assignment #7の採点結果です。遅れて申し訳ありませでした。
今回は
半径RのGrounded hollow sphere内に中心点から距離aの場所に点電荷qがある時のPotential問題をmethod of imageにより解く。
(i) 境界条件を満たす「Image電荷の大きさと位置」を導出するプロセスを論理展開の筋道がわかるように簡潔に書く、
(ii) hollow sphereの内壁に誘起される電荷分布σ(θ)の表式を求める。
(iii) 得られた結果をもとに、等電位線、電気力線、内壁に誘起される電荷分布が描かれた図を描く。
という問題でした。
採点基準は
(i) 境界条件を満たすImage電荷の大きさと位置をきちんと導出できている。(2点)
(説明が不十分なものは1点)
(ii)誘起された電荷分布σ(θ)が計算できている。(1点)
(iii)等電位線、電気力線、電荷分布が描けている。(2点)
(電荷分布が描いてないなど、不十分と感じたものは1点)
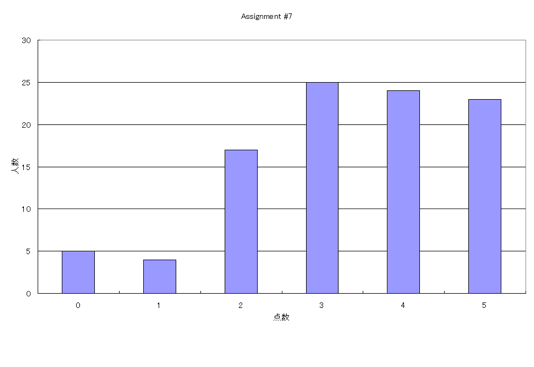
と、5点満点にしました。
以下、気づいた点を述べます。
・(ii)の問題で、符号を間違えている人が非常にたくさんいました。
Gaussの法則を用いて電荷分布を求めたと思いますが、今回の場合は球の外側は全て導体になっていますので、normal derivativeの向きは球面の内向きになります。
・(iii)の電気力線を描く問題で、球を貫いて書いている人が大部分でした。
理解しているだろうと思い一応正解としましたが、実際の電荷とimage電荷だけが存在すると思えば確かにそのような図になりますが、この問題では球の外は導体なので電気力線は浸入しません。
Assignment#8(後期#3)(10/31)
「帯電した物体に(最初は帯電していない)紙切れがなぜ、引き寄せられるか?」に対する説明を、授業で講義した内容を用いて、簡潔に与えることをAssignment#8(後期#3)として設定しました。図と式を含む簡潔な(読んですぐにわかる)文章からなるレポートが要求されている基準です。
今回の問題は、「帯電した下敷がなぜ紙を引きよせるのか」という、「静電気」の一言で片付けられてきた問題を、物理的に説明せよというものでした。
ポイントは、双極子モーメントと電場の向き、そして力(トルク)の働く向きです。
電場の向きに分極が生じ、電場と電気双極子の相互作用によって力が働きます。
このとき、この力は電場に比例します。これは、帯電した物体の電荷が入れ替わっても変わらないことに注意してください。
これらのポイントを抑えている解答はマルにしました。
多くの人はよくできていたと思います。
わからなかった人はもう一度復讐しておいてください。
今回のAssignment#8(後期#3)は返却しません
-----------