Assignment#1(前期1回目:4/17/2007)
(問題1)
距離の逆二乗則を示す力として電気力(クーロンの法則)と重力(万有引力の法則)がありますが、水素原子のエネルギー準位を考える際(atomic scale)には電気力のみを考え、原子核と電子の間に働く重力は考慮しません。逆に太陽系における地球の公転運動を考える際(macroscopic scale)には太陽と地球の間に働く重力のみを考え、電気力は考慮しません。それはどうしてなのか?をこれらの系における電気力、重力を見積もり、説明せよ(日本語として、論理展開がはっきりわかるように書かないと採点できません)。
<出題意図は授業LOGを参照せよ>
<早川TAによる総評>
問題の性質上採点基準が少しあいまいになっていますが、一応以下に示します。
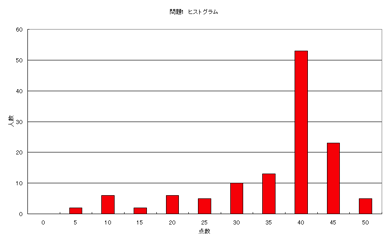
水素原子、太陽−地球の場合で25点ずつ、合計50点満点です。
・水素原子に関して、重力・電気力どちらか片方だけ見積もり、結論を述べている。(15点)
・水素原子に関して、重力・電気力をともに見積もり、そこから結論を導いている。(25点)
・太陽−地球に関して、重力だけを見積もったところでやめてしまっている。(15点)
・太陽−地球に関して、重力を見積もり、何らかの理由を考えて結論を述べているが不十分な場合。(20点)
・太陽−地球に関して、重力を見積もり、さらに電気力を無視していいきちんとした理由を説明している。(20点)
といったところです。以下何点か思ったところをコメントさせていただきます。
・水素原子の問題はよくできていたと思います。しかし、細かい計算間違いが多かった気がします。今回の問題では細かい数値は気にしないことにしましたが(オーダーにして2,3桁)、気をつけましょう。
・太陽−地球の問題については、二つの天体の電荷が分からないからでしょうか、途中で計算を止めてしまっている人が多くいました。もったいないですよ。もっと考えましょう。
・また、天体の電荷はほぼ0とみなせるから電気力は考えないとしている人が多かったです。この回答で満点をあげてもいいかと思いましたが、さらに一段階深く考えて回答してくれている人もいたので、差をつけるために5点引かせてもらいました。
・電気力、重力どちらか片方だけを見積もり、その値が大きいから・小さいからという理由で結論を述べている人が多くいました。物理量の大小を述べる際は常に他のものと比べて大きい・小さいといわなければなりません。気をつけましょう。
・距離rと比べて質量m、電荷qが大きい・小さいからということを書いている人がいました。クーロンの法則・万有引力の法則ともに距離の逆二乗に比例するもののはずです。距離rとの大小を比べてもそれはどちらの力にもいえることのはずですから、この比較は意味がありません。
-------------
(問題2)
問題2.7を解け。これらの答えは1年生の物理学でガウスの法則を用いて計算したことがあると思いますが、ガウスの法則を使わずに積分(式2.7)で計算してください。ガウスの法則で計算しても採点はゼロにします。
<佐藤TAによる総評>
今回の問題は、「半径Rの球殻の表面に一様な電荷密度σで電荷が分布しているとき、球の中心からz離れた点における電場を、全電荷qを用いて表せ。ただし、ガウスの法則を使ってはならない。」というものでした。
採点基準は、
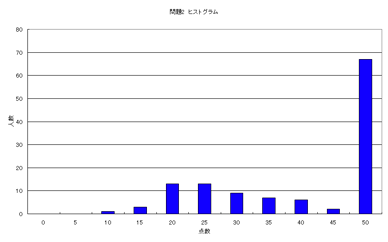
・電場がz軸方向にしか発生しないことに気付き、z軸方向にクーロンの法則を適用できている(25点)
・z < Rのときの電場を、積分を実行した上で求めている(12点)
・z > Rのときの電場を、積分を実行して求め、全電荷qを用いて表している(13点)
で50点満点で採点しました。
半分以上の人がほぼできていましたが、中にはほぼ白紙に近い答案も見受けられました。
今回できなかった人は、わからないところをハッキリさせた上で質問にくるなどして、わからないところを解消してください。
以下に気になったことを挙げます。
・電場はz軸方向にしか発生しないことを、積分を実行した上で証明してくれた人もいました。今回は球対称から自明かなと思い、採点基準には加えませんでしたが、やってない人はぜひ一度やってみてください。
・答案の中には、球の「内部に」一様に電荷密度σで電荷が分布しているとして解いているものもありました。これらの答案もあっていた場合にはマルにしました。
・また、ポテンシャルを求め、zで微分して電場を求めている人もいました。これも、あっているものはマルにしました。(注:ポテンシャルのみ求めて終わり、な答案もいくつかありましたが、これは今回の題意にはあわないので、完全なマルはあげていません。きちんと電場まで求めてください。)
・電荷密度を全電荷qに直していない人がいましたが、題意を考慮し、点数を1点引きました。
・全体的に、立式の問題というよりは、積分計算ができるか否かで、大きく差が出たように思います。数学は物理をやる上で必要最低限です。せめて置換積分、部分積分くらいはできるようになっておいてください。
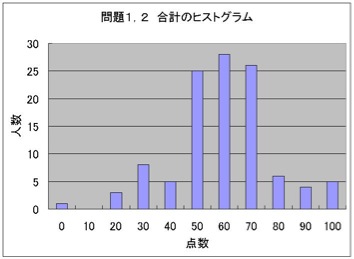
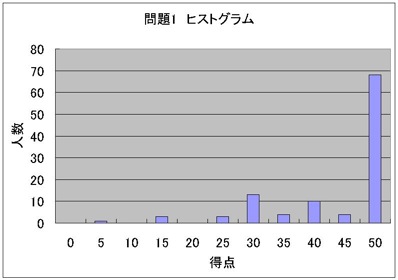
(問題1&2のヒストグラム)
質問受付は、本来なら5/4(金曜日 夜間3-4時限(17:50-19:20)@1138 教室ですが、お休みなので、今回に限り、
5/2(水曜日)夜間3-4時限(17:50-19:20)に7F物理事務室となりの特別実験室でTAが待機していますので活用してください。
Assignment#2(前期2回目:5/1/2007)
(問題1)
一様に帯電した半径Rの球(全電荷量はqとする)のポテンシャルの表式V(r)を以下の二つの方法で求め、グラフでその概形を示せ。ここで、r は球の原点からの動径距離である。
(i)問題2.8で既に求まっている電場Eの表式をもとに式2.21にしたがい「計算し易い経路」を設定し線積分を計算することによりポテンシャルを求める:「ポテンシャルの基準点」および「計算し易い経路」はどのように取ったか?明記せよ)
(ii)式2.29にしたがい体積積分を計算することによりポテンシャルを求める:式2.29では「ポテンシャルの基準点」はどのように取っていることになっているか?明記せよ)
<佐藤TAによる総評>
今回の問題は、
一様に帯電した半径Rの球(全電荷量はqとする)のポテンシャルの表式V(r)を以下の二つの方法で求め、グラフでその概形を示せ。ここで、r は球の原点からの動径距離である。
(i)問題2.8で既に求まっている電場Eの表式をもとに式2.21にしたがい「計算し易い経路」を設定し線積分を計算することによりポテンシャルを求める:「ポテンシャルの基準点」および「計算し易い経路」はどのように取ったか?明記せよ)
(ii)式2.29にしたがい体積積分を計算することによりポテンシャルを求める:式2.29では「ポテンシャルの基準点」はどのように取っていることになっているか?明記せよ)
というものでした。
採点は、
(i)
式2.21が適用できている(11点)
「ポテンシャルの基準点」を明記している(4点)
「計算し易い経路」を明記している(4点)
答えがあっている(6点)
(ii)
式2.29が適用できている(13点)
「ポテンシャルの基準点」を明記している(6点)
答えがあっている(6点)
で50点満点で採点しました。
前回の問題を復習していた人は、今回の(ii)の積分は計算できていたようでした。
前回から比べていきなり点数が上がった人もいて、質問にはこないけど自分で解決している、という印象を受けました。
以下、気づいたことを挙げます。
・今回は、計算はよくできているようでしたが、物理的意味や条件がおろそかになっている人がかなり多く、惜しくも満点を逃していました。特に、(ii)で、式が(i)と同じになることには気づいているのに、ポテンシャルの基準点がどこにあるのか、明確になっていない人が多いようでした。
・また、一様に帯電した球でなく、一様に帯電した球殻で解いている人もいました。合っていた場合には点数をあげましたが、前回も同じように状況を勘違いしている人がいました。問題文を落ち着いてよく読んでから取り組んでください。
・求めたポテンシャルのグラディエントをとって、元の電場に戻るか確かめている人もいました。結果を見直し、考察するのはとても大切なことですので、これからもその努力を続けてください。
以上です。
わからないことは、どんなことでも遠慮なく質問にきてください。
******************
今回のレポートの中には、特定の人物が中心となってグループで一言一句完璧に同じ(縮退)
になっているものがいくつか見受けられました。
テストと違って、誰にも相談するなとは言いませんが、教えてもらった内容をせめて自分で咀嚼してから
レポートにしてください。
******************
-------------
(問題2)
一様な表面電荷密度σで帯電した無限に広い平面板の作る電場をガウスの法則を用いて4月24日(第2回目)の講義で求めたが、立体角(Solid Angle)を用いた議論で同様に求めてみましょう。(論理展開をはっきりわかるように書いてください)
<早川TAによる総評>
今回の問題は、
一様の電荷面密度σで帯電した無限に広い平行板の作る電場を、ガウスの法則を
用いる代わりに立体角(solid angle)を用いて求めよ。
というものでした。
採点基準は、50点満点中
・微小立体角要素dΩを導出できている。(20点)
(きちんと立体角の説明をしていないものは−5点)
・微小面積要素dSが作る電場dEを導出できている。(20点)
・上の二つを結びつけて電場Eを計算できている。(10点)
(積分範囲について触れていないものは−5点)
といったところです。
今回の問題では、dΩを考えるときとdEのz成分(面に対して垂直方向)を考える
際にcosθ(θはfield pointを球座標の原点に取ったときのrベクトルと平面の法
線ベクトルの成す角)が現れてキャンセルするのですが、これを考慮しなくても
問題は解けてしまいます。そのような解答は点数を半分にさせてもらいました。
気をつけてください。
以下、気がついた点を述べます。
・せっかく立体角で考えているのに、その後球座標に変換して積分をしている人
が多かったです。
確かに間違ってはいないのですが、立体角のパワフルさを実感できなかったの
ではないでしょうか?
立体角を使うことの利点を考えましょう。
・多くの人は座標の設定が雑でした。どこを原点として、何座標系で考え、この
記号は何を意味するか、ということを分かりやすく書くようにしましょう。
・この問題は、通常電場のz成分のみを考るだけでよいのですが、その理由につ
いて触れていない人が多かったです。
対称性から、とだけ書くのも少し乱暴です。何が、どのような対称性を持って
いるから、こう考えられる、という論理の展開をするようにしましょう。
(何も述べずにz成分だけ考えているものは−5点させてもらいました。)
・まだ慣れていないせいでしょうか、ベクトル=スカラーという式を書いている
人がよくいます。2つの性質の違いをよく理解しましょう。
場合によってベクトルで書くのか、ベクトルの成分で書くのかをきちんと使い
分けましょう(はっきりと文章で、こちらを使う、と書くのもよいでしょう)。
---------------------
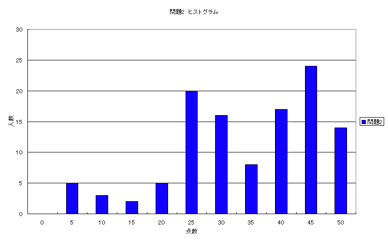
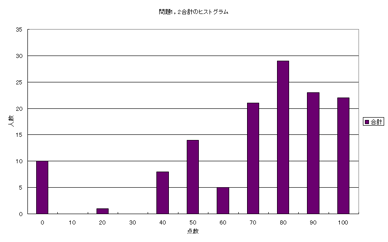
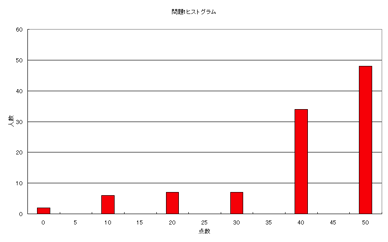
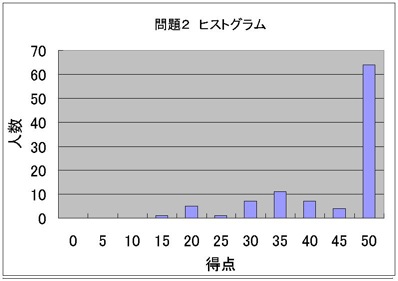
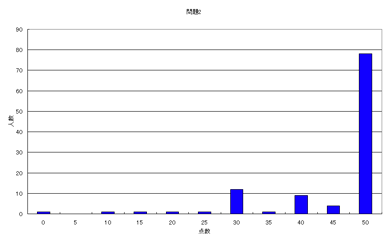
(問題1&2のヒストグラム)
今回の質問受付は、5/18(金曜日) 夜間3-4時限(17:50-19:20)@1138 教室です。
assignmentの問題だけに限らず電磁気学関連の質問もwelcomeですので、このTAによる質問受付を活用してください。
Assignment#3(前期3回目:5/22/2007)
(問題1)問題2.34を解け。半径aおよびbの球殻が持つ自己エネルギーは?、Cross-Termは?、No superpositionは?に注意して単なる計算に留まらないよう、読んでわかる解答を準備してください。
<佐藤TAによる総評>
採点基準は以下の通りです。
(a)
式2.45が適用できている(5点)
電場がそれぞれの領域で求まっている(10点)
積分範囲に気を付けながら、静電エネルギーが求まっている(5点)
(b)
それぞれの球殻の静電エネルギーが求まっている(14点)
cross-termが求まっている(7点)
全静電エネルギーが求まっている(7点)
No superpositionについて言及している(2点)
以下、採点していて気になったことを書きます。
・ガウスの法則から、電場を正しく求めることができずに、その後の公式の適用方法は合っているのに答えが違う人が何人かいました。いままでやったところでわからないところや曖昧なところがあったら、解決しておいてください。
・前回のAssignmentの課題だった、仕事からエネルギーを求める方法で、答えを検算している人がいました。
さまざまなアプローチを試みることは、物理を考える上で非常に重要になります。他のみなさんも別解が思い付いたらどんどん書いてください。
・半数以上の人が、計算のみで終わっていたのは残念に思いました。みなさんがやっているのは数学ではなく物理なので、計算結果についてもう少し物理的に考えてみてください。そうすれば、自ずと自分の計算ミス等に気づくはずです。
---------------------
(問題2)MIT Open Course Ware電磁気学VideoLectureの8( 42分〜)を使い、料理鍋の外側から電荷を与えると料理鍋の電位は直ぐに飽和してしまい電荷を移すことが出来なくなってしまいますが、鍋の内側から電荷を与えると電位は直ぐに飽和することなく(空気中でコロナ放電が起こるまでの電位になるまで)電荷を移すことができることを見てもらいました。これはVan de Graff 発電機の動作原理に他なりませんが、どうしてこのようなことが起きるか?を自身の言葉で書いてください。
<早川TAによる総評>
この問題の本質としては、料理鍋と帯電球が理想導体であることを仮定すれば、
導体の性質からこの現象の説明ができるはずです。
というわけで、採点基準は非常にあいまいなのですが、以下のとおりです。(50
点満点)
・導体の性質から、それぞれの状況での電荷分布を説明し、電位の評価をして解答している。 50点
・導体の性質から、電荷分布の説明はできているが、そこからの議論があいまい。 30点
・それぞれの状況でおきている現象(電荷の分布など)を説明はしているが、それがなぜ起こるのか説明していない。 10点
といったところでしょうか。自分の予想より点数が低かった方は、なにか説明が
足りなかったと考えてください。
以下、気になったところを何点か述べておきます。
・電圧と電位を混同している方が多くいました。電位はある点(通常は無限遠方)を基準にした静電ポテンシャルで、電圧はある二点間の電位差です。確かに基準点との電位差と考えれば電位を電圧と呼んでもよいかも知れませんが、あまり意味のないことです。気をつけましょう。
・assignment問題1との類似から、帯電球を内側から近づけた時の状況を自己エネルギーの大小で説明していた方がいました。
確かに帯電球を鍋に接触させる前後の自己エネルギーの大小を評価することはできますが、実際にはその間に帯電球を接触させるという過程があります。
その過程を考慮するためには、帯電球を鍋に接触させる直前の自己エネルギーと、そこから無限小だけ位置を変化させて鍋に接触させた直後の自己エネルギーの大小を比較しなければならないでしょう(その際電荷の移動は一瞬で起こるものとします)。
そこまで厳密な解答をしてくれた方はいなかったので、自己エネルギーを用いた解答には一律20点つけました。
・静電容量と電圧の関係から説明している方がいましたが、その議論は2つの導体が存在して成り立つものでしょう。
調理鍋と帯電球を接触させた瞬間に二つの導体は一つになったとみなすことができ、電位差はなくなるので静電容量のみで説明することはできないと思います。
・導体の性質から電荷が鍋の表面にどのように分布しているかは説明できているのですが、その後+の電荷が表面にたくさんあるから
外側からだと電荷が入らない、内側は電荷がないから入る、としている方が多くいました。後半の議論が大雑把です。
確かに本質的に起こっていることはそうなのでしょうが、電位という概念を用いて説明したほうが分かりやすいでしょう。
・鍋の外側から帯電球を近づけると、電荷が偏って分布するから多くの電荷を加えられない、と説明している方が意外と多かったです。
もう一度導体の性質をよく理解したうえで考えてみましょう。
帯電した導体中では、導体内部に電場を生じさせないように電荷が分布します。
それを踏まえた上で、この場合は鍋の表面に一面に分布するということを理解しましょう。
---------------------
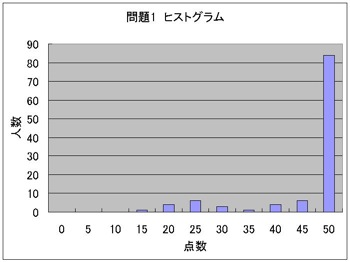
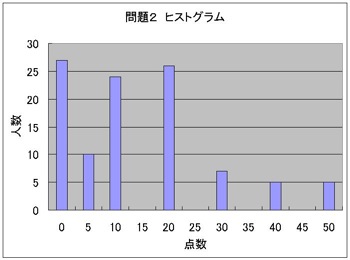
(問題1&2のヒストグラム)
今回の質問受付は、6/8(金曜日) 夜間3-4時限(17:50-19:20)@1138 教室です。
assignmentの問題だけに限らず電磁気学関連の質問もwelcomeですので、このTAによる質問受付を活用してください。
Assignment#4(前期4回目:5/29/2007)
(問題1)C11,C21の具体的な計算
<早川TAによる総評>
今回の問題は、中心が同じ2つの球殻を考え(球殻1、2とします)、その半径を a, bとしたときの容量係数 C11, C21を求めるというものでした。
みなさん大変よくできていたと思います。ですが、採点基準の前にまず皆さんに注意してもらいたいことがあります。計算をする際に自分がどのような仮定をおいているか(どのような状況を仮定しているか)、を常に意識してほしいということです。
今回の問題では容量係数と球殻 1、2の電荷 Q1, Q2, 電位 V1, V2 の間に、
Q1 = C11*V1 + C12*V2
Q2 = C21*V1 + C22*V2
という関係が成り立つでしょう(容量係数の定義)。
容量係数が導体の配置のみで決定される定数であることを考えると、この式から分かるとおり各球殻の電位を決定すれば各球殻の電荷が決まり、逆に各球殻の電荷を決定すれば電荷も一義的に決定されるはずです。
さて、実際にこの問題を解くにあたっていろいろな状況設定をしたと思います。もちろん上式のまま解いていっても求められますが、より簡単に解くために
・Q1を0として、Q2に電荷を与える(V1, V2は未知)。
・Q1に電荷を与え、Q2を0とする(V1, V2は未知)。
・球殻2を接地して、V1を与える(Q1, Q2は未知)。
・球殻1を接地して、V2を与える(Q1,Q2は未知)。
というような仮定をすると楽かと思います。導体の配置が変わらなければ容量係数も変わらないので上のような状況で計算してもOKでしょう。
ここで気になったのは、電位(電荷)を与えた上でさらに電荷(電位)を任意に決定しているような表現をしている方が多数いました。例えば、もっとも多かったのが外球殻を接地して内球殻に電位Vを与えたときに、内球殻に+Q帯電して、外球殻に-Q帯電するということをなんの断りもなく書いて
いる方です。確かに少し計算をすればすぐに求められるので自明としてしまってもよいようなものですが、なんの説明もなくこうしてしまうのは少し乱暴な気がします。というわけで、このような解答は10点引かせていただきました。
上の例のような仮定の元に計算している場合、自分が今コントロールしているのは2つの球殻の電位であって、電荷はそれに伴って自動的に決定されてしまうのでコントロールすることはできません。最初に自分がどのような状況設定をしたのか、計算の途中でも常に意識していてください。
その他にもどこを電位の基準に取っているのか、どこを接地しているのか分からない解答や、最初の仮定に途中で矛盾するようなことが書いてある解答は減点させていただきました。
というわけで、採点基準(というか減点対象)は(50点満点)
・自分の状況設定と矛盾するような表現をしている。 -10点
・計算間違い -10点
といったところでしょうか。大きく減点されている方は上の対象がいくつかあっ
たものと思ってください。
(問題2)C12,C22の具体的な計算をして、求めた容量係数C11,C12,C21,C22の表式を(C={C11C22-C12^2}/{C11+C22+2C12})に適用して得られるCの表式が例題2.11のCの表式と同じになるか?をcheckする
<佐藤TAによる総評>
今回はいままでの知識を組み合わせて解く問題でしたが、きちんと前回までの内容が理解できているようで、
とてもよく出来ていたと思います。
今回の採点基準ですが、
・C21,C22が正しく導出できている(32点)
・Cが正しく導出できている(18点)
で採点しました。
僕が気づいたことの半分以上は早川TAが熱弁してくださっているので、2点だけ指摘しておきます。
・問題1と2でつながっていたせいか、文字の定義や計算過程を書かずに、結果だけ並べている答案が全体の1/3以上でした。「人に伝える」ことをもう少し意識して、丁寧に書いてください。
・また、多くの人は、「接地されている」ことと、「ポテンシャルの基準点」を混同しているように見受けられました。そのことに気づき、正しい解答を導いていたのはただ一つだけでした。
※ポテンシャルは基準点を定めた上で相対的に測れるものであり、クーロン場の場合には無限遠を基準とすると無限遠でポテンシャルがゼロになるためにそう置いていますが、本来その基準点は任意です。気づかずに解けてしまった人は、自分のポテンシャルの基準点をもう一度見直してみてください。
以上です。
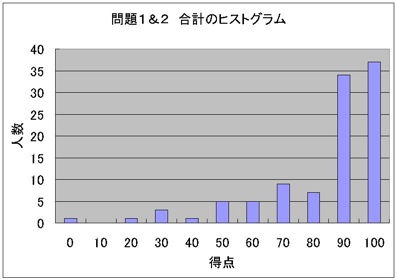
---------------------
(問題1&2のヒストグラム)
Assignment#5(前期5回目:6/12/2007)
(問題1)授業で解説したp227のExample5.9(Solenoid Coil)では半径Rの円筒形に巻かれたコイルを考えているが、その断面が円形でない(金太郎飴のようにどの場所でも断面の形は同じ)Solenoid Coilを同様に想定し、コイルにより作られる磁場を求めよ。
<佐藤TAによる総評>
得点分布からもわかるように、今回はできた人とできていない人の差が大きく出たように思います。
アンペールの法則は、今回の問題からもわかるようにとても強力で有効な法則です。
今回の問題がわからなかった人は、よく復習しておいてください。
今回の採点基準ですが、
・動径方向の成分が0であることを証明している(10点)
・方位角(Φ)方向の成分も0であることを証明している(10点)
・コイルの外側でのZ成分が0であることを証明している(15点)
・コイルの内側でのZ成分を求めている(15点)
以下に気づいた点を挙げます。
・多くの人は、電流を反転させたときとZ軸を逆転させたときの結果との矛盾から動径方向の成分がないことを証明し、
その後方位角方向に関してAmperian Loopを考えることでZ成分しか持たないことを示していましたが、中にはビオ・サヴァールの法則から、磁場はZ成分のみしか持たないことを示した人もいました。(その後の計算はアンペールの法則を使っていました。)
ビオ・サヴァールの法則からも同じ結果が得られるはずですが、その積分計算はとても複雑になります。
今回、矛盾からZ成のみであることを示した人は、ぜひビオ・サヴァールでも途中までやってみた上で、アンペールの法則の強力さを実感してください。
・動径方向が0であることを示すのに、「対称性より」の一言で片付けている解答がいくつかありました。また、磁場の方向はZ軸方向のみであるとして、Z軸方向の磁場のみ計算している解答もいくつかありました。これらは、上の採点基準に従って減点しました。
・断面が対称性のある形をしていないため、方位角方向のAmperian Loopを考える際に、斜め上に登る電流を射影した成分を考え、それがコイルの巻数を大きくしたときにゼロとみなせることを示していた解答もありました。
(問題2)半径aの円柱を軸方向に一様に流れる電流分布(全電流をIとする)の作る磁場を求め、その磁場がすべての点で場の方程式 ∇×B=μ0*J を満たしていることをcheckせよ。
<早川TAによる総評>
今回の問題は
半径aの円柱を軸方向に一様に流れる電流分布(全電流をIとする)の作る磁場を
求め、
その磁場がすべての点で場の方程式 ∇×B=μ0*J を満たしていることを
checkせよ
という問題でした。
全体的な感想としては、非常によくできていたと思います。
採点基準は
・円柱の内部、外部での磁場を求められている (各15点)
・円柱の内部、外部での場の方程式の成立を確認できている (各10点)
です。計算間違いなどは−5点されているはずです。
以下、気づいた点です。
・まず、どの座標系を使って計算しているのかよく分からない人が多数いました。
できれば最初に何々座標を用いて考える、と宣言したほうがよいでしょう。
・多くの方がアンペールの法則を用いて磁場を計算していましたが、これを用い
る際の注意点は
問題1のコメントに書いてあったものとほぼ同じです。何もコメントせずに磁場
の方向を決定している方は
説明不足だと感じました(減点はしていませんが)。
ガウスの法則もそうでしたが、アンペールの法則も用いる際はまず系の対称性
をきちんと考慮して、
磁場のベクトルが持ちうる成分を限定しなければなりません。公式を使って計
算するのはその後です。
・アンペールの法則を用いる際にAmperian loopを考えるわけですが、どのよう
なloopをとっているのか
よく分からない回答がいくつかありました。きちんと意識しましょう。
・磁場のcurlを計算する際に、直交座標系(もしくは極座標)の形式をそのまま
円柱座標に用いている方が
意外と多かったです。その場合円柱座標から直交座標に戻すか、円柱座標での
curlで計算しましょう。
ちなみに、教科書を開いてすぐのところに各座標系でのgradient, divergence,
curlがまとめてあります。
活用しましょう。
・ 円柱外での∇× Bを計算して、0になるのでそこでは場の方程式が成り立ってい
ない、
と解答している方が多数いましたが、円柱外ではJ = 0 なのでそこでも場の
方程式は成立しています。
減点はしていませんが気をつけましょう。
--------------------
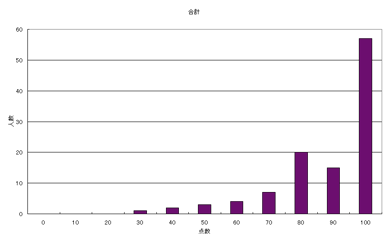
(問題1&2のヒストグラム)
Assignment#番外編[1](6/26/2007)
(問題)授業LOGを参照