09月26日(第01回目)の講義
10月03日(第02回目)の講義
10月10日(第03回目)の講義
10月17日(第04回目)の講義
10月24日(第05回目)の講義
10月31日(第06回目)の講義
11月07日(第07回目)の講義
11月14日(第08回目) の講義
11月21日 休講
11月28日(第09回目) の講義
12月05日(第10回目) の講義
12月12日(第11回目) の講義
12月15日 補講(第12回目) の講義
12月19日(第13回目) の講義
12月22日 補講(第14回目) の講義
1月16日 休講
9月26日(第1回目)の講義では
3章Special Techniquesに移りました。3章では、前期に勉強した「静電場」の問題について、偏微分方程式であるラプラス方程式の解法や鏡像法といった技法を中心に学びます。
なお、2006年度の電磁気学の授業LOGに事前に目を通しておくと、おおよその流れがわかって、予習をしたい時には利用できると思います。(講義LOGを書く際に、昨年のものを参照しますが、あたらに加筆する事項はあまりない状況です)
今年度で、電磁気学の担当は終わりです。2004年度〜2007年度(4年間)担当したことになりますが、そろそろ講義にたいする新鮮さが失われつつある感覚を持っていたので、別の授業を担当するのがちょうど良い頃だと思います。数年間はもう電磁気学を教えないと思うと、残りは半年ですが、出来るだけ良い授業を提供できるようにしたいと思います。
(1)これまで扱って来た静電場の問題は与えられた電荷分布がどのような場やPotentialを作るか?を積分により求めるものでしたが、例えば、導体に与えた全電荷量Qはわかるがそれがどのような表面電荷分布をするかは(導体の形状に対称性が無く)自明でない場合や、電源を用いて導体の電位(Potential)自身を制御する場合は、これらの積分の方法は使えません。電荷分布がelsewhereにはあるが、それを除いた電荷のない空間でのPotential V(r)を知るためにはLaplace方程式∇^2V(r)=0という偏微分方程式を適切な境界条件(Boundary Condition)で解くことになることを説明しました。 電荷密度分布を右辺にソースとして持つ「ポアソン方程式」と何が異なるか?物理数学で学んだ偏微分方程式の視点から説明できるようにしましょう。
(2)電荷のない空間でのPotential V(r)が満たしている特徴的な性質(The value of V at the point r is the average value of V over a spherical surface of radious R)を、テキストp114にあるように、点電荷の作る場について、積分計算をしてcheckしてみることを指示しました。点電荷の作る場についてこの点がcheckできれば、重ね合わせの原理により、任意の電荷分布が作る電荷のない空間でのPotentialについても成り立つます。
(3)『電荷のない空間でのPotential値はそのまわりのPotential値の平均値になっているという、静電Potentialの満たす性質』を(2)では静電場の基本であるクーロンポテンシャルをもとにして、いわば天下り的に確かめましたが、当然、Laplace方程式∇^2V(r)=0という場のでき方を記述している偏微分方程式のなかに、その性質を直接読み取ることができるはずです。そこで、(簡単のため)2次元の格子化したLaplace方程式を用いて「格子点(i,j)における電位は、まわりに隣接する4つの格子点の平均値に等しくなるように決まる」ことをLaplace方程式が要求!していることを確かめました。それを実践した解法がRelaxation Method(緩和法)ですが、それをQuickTime Movieで見せました。
2次元直交座標系で4辺の電位(境界値)が与えられた例題
(電磁気web-pageの『電磁気学webコンテンツ集』から)
計算例[T字型の境界条件を例にとって]
(電磁気web-pageの『電磁気学webコンテンツ集』から)
(4)Laplace方程式が要求!している場のでき方からは、「空間に電荷を含まない静電場を考えると、電位はその領域内において極大値、極小値も取らない」というEarnshaw(アンショウ)の定理が導かれるという話をしましたが、演習で扱う問題3.2(p115)を解いて、「electrostatic containment is out of the question」 を体感してください(『電磁気学webコンテンツ集』にその助け?になるマテリアルがあります)。
ポテンシャルで見るEarnshawの定理、Problem 3.2(ElectroStatic Bottle)から
(電磁気web-pageの『電磁気学webコンテンツ集』から)
(5)Relaxation Method(緩和法)を適用した四角パイプの問題を、変数分離によりLaplace方程式を解く方法で解析的に扱いました。(これは問題3.14(p136)の問題そのものです:ただし辺の長さa,bが逆になっています)最後のV(x=a,y)=V0の境界条件をそれまでに求まった解の和として満たさなければならないこと、それ自身が方形波のフーリエ級数になっていることを指摘しておきました。
2次元直交座標系で4辺の電位(境界値)が与えられた例題
(電磁気web-pageの『電磁気学webコンテンツ集』から)
(6)四角パイプの問題では変数分離法の方法を直交座標系で用いましたが、球座標系ではどうなるか?自由空間で導体球の電位を指定した場合には電位は球対称性(Vは動径長rだけの関数)を持ち、偏微分方程式は簡単に解ける話をしていて時間切れです。
(7)次回は球座標系での変数分離法について話を(p137)します。物理数学2で学習した「Legendre(ルジャンドル)特殊関数」について復習しておいてください。
10月3日(第2回目)の講義では
ラプラス方程式の極座標系での変数分離法による解法の話をしました。
(1)一様外電場中に置かれた導体球を扱うExample3.8(p141)を取り上げました。起こる現象は、
導体球の表面には一様外電場により表面電荷σ(θ)が誘起され、その誘起された表面電荷σ(θ)が新たに電場を導体球の外ばかりでなく内部にも作り出し、その結果として誘起電場と外電場の和からなる場は(i)導体表面に垂直にその電気力線が向き(ii)導体内の電場がゼロになる、というものです。
(2)この現象を定量的に議論するために、導体球の外側の空間を考察の対称として極座標系におけるラプラス方程式を変数分離法により解きました。球対称性がなく、一様外電場方向のz軸まわりの軸対称性しかない場合には、極座標系の角度θにも電位が依存し、V(r,θ)の一般解が式3.65になること(物理数学2で学習済みの話)からスタートして、導体表面を内側の境界として持ち無限の彼方を外側の境界として持つ領域について境界条件(境界における電位)を課して求まったポテンシャルの表式は、一様外電場のポテンシャルと誘起電場のポテンシャルの和になっていることを確認しました。
(3)さらに、誘起された表面電荷σ(θ)の表式をσ=-ε0*∂V/∂n により求めてみると、直感的にはもっともらしい「三日月型?」の分布が得られました。
(4)Example3.9(p142)を取り上げ、球面上の電荷分布σ(θ)が最初に与えられた場合をテキストの記述に沿って解説しました。この問題では半径Rの球の外側(OUT)と内側(IN)を分けて考えました。OUT領域とIN領域の境界条件を、Laplace方程式という偏微分方程式の境界値問題としてどのように与えたか?(境界における電位を与えたのか?/境界に置ける電位の垂直微分を与えたのか?/なぜ外側(OUT)と内側(IN)の境界値問題を抱き合わせで考えたのか?)について今一度整理してみてください。
(5)この問題の解法で用いた論法の理解を深めるためにAssignment#1を出しました。
半径Rの球殻に大きさσ0の一様な表面電荷分布を与えたときのポテンシャルを球殻の内側および外側で求める問題です。答えは自明ですが、ここで問っているのはExample3.9で扱ったと同じく、境界値問題を解くという論法で回答を書くことです。TAの人は論理構成がわかるように書いてあるかどうかだけを大雑把に採点します。授業中にしつこく言いましたが、間違っても3.83式から出発して答えを書くということのないように(そのような場合はゼロ点と採点します)。
(6)p145問題3.25&3.24は、本来ならAssignment#1として出したかった問題ですが、円柱座標系における同様なLaplace方程式境界値問題です。各自で計算してみてください(答え合わせとして、誘起される電荷はσ(φ)=2(ε0)(E0)Cos(φ)となります)
(7)授業後の質問で感じましたが、Legendre(ルジャンドル)特殊関数に難しいという印象を持っている人が少なからずいるようです。直交関数系の話(線形代数におけるベクトル/基底ベクトル/成分/内積/直交性が直交関数系ではどうなっているか?)をしっかり復習をしてください。
(8)次回はテキストp121 の Method of Imageに入ります。
10月10日(第3回目)の講義では
静電場の境界値問題を解く方法として、3章で学んで来た、Relaxation Method(緩和法)、変数分離法に加え、「複素関数を利用する方法」と「Method of Image(鏡像法)」を解説しました。
(0)Assignment#1(後期)の解説をしました。
(1)「複素関数を利用する方法」の解説をしました。
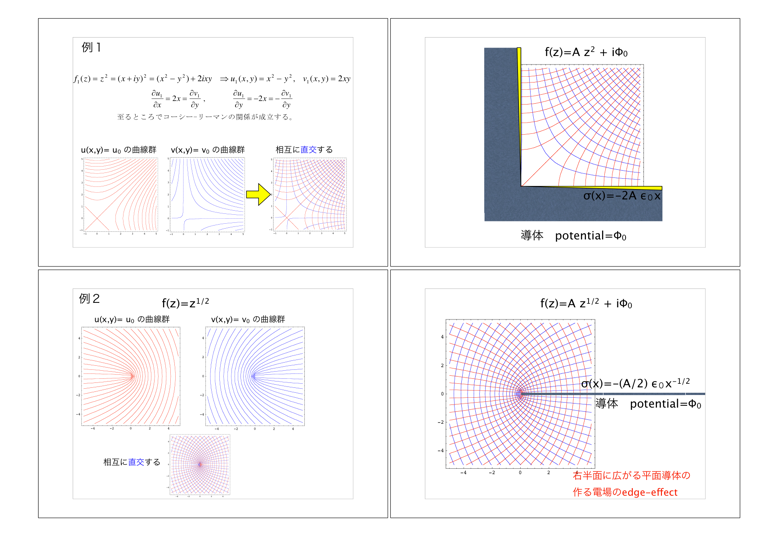
物理数学2で既に学習した複素関数f(z)について、解析的(正則)な場合(z2は正則ですが、z*は正則ではありません。正則でない例として授業ではabs(z) と言ってしまいましたが訂正です)には、複素関数f(z)の実部u(x,y)と虚部v(x,y)は無関係ではなくコーシーリーマンの条件を見たし、それゆえ実部と虚部それぞれがラプラス方程式を満たす解になっていること、u(x,y)=u0の曲線群とv(x,y)=v0の曲線群は相互に直交することを確認し、「複素関数を利用する方法」について、f(z)=z2, z 1/2 が使える例について解説しました。この方法は解くべき境界に合う複素関数f(z)を数多く知っていることが必要ですが、複素関数論に出てくるConfromal Maping(等角写像)と密接に関係しています。興味のある人は、是非、勉強してみてください。
(2)「Method of Image(鏡像法)」を解説しました。、Method of ImageをWikipediaで調べてみると「The method of image charges (also known as the method of images and method of mirror charges) is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.」 となっていますが、その典型例として「Grounded conducting planeと点電荷qからなる系(Original Problem)のPotential問題」p121を取り上げました(電磁気のテキストでmethod of imageを扱っている場合には例題として必ず掲載されています)。
(Original Problem)と似て非なる[点電荷qとImage点電荷q’(導体はありません)]からなる系(Analog Problem)を利用して、z=0の境界面でPotential=ゼロという境界条件を満足するようにImage点電荷q’の大きさと場所を決め、解く方法がMethod of Imageです。導体表面に誘起される電荷分布σ(ρ)は問題が解けるまではあらかじめわかりませんが、Potential問題が解けたあとはNormal derivativeにより求めることができ、直感通り点電荷に最も近いρ=0で最大値をとり、対称軸まわりの回転角θには依存しない、全電荷量がImage点電荷q’に等しいσ(ρ)が求まりました。点電荷に働く力についても電荷分布σ(ρ)が点電荷の場所に作る電場を計算し求め、それが点電荷qとImage点電荷q’を考えた単純な結果と一致することも確かめました。ただし、この系に蓄えられた静電場エネルギーについて単純に(Analog Problem)の答えを代用してはまずい点について言及しました。
(3)(2)の例では、Image点電荷は1個で十分でしたが、複数のImage点電荷が必要で、常に境界条件を満足するようなImage点電荷q’の置き方があるわけではないことを体感するために、p126の問題3.10を考えてみました。90°の場合、45°の場合、135°の場合について解法の方針と、なぜ角度が限られるのかについて絵解きで説明をし、Method of ImageではPotential問題を考えている空間にImage点電荷を置いては行けない(Original Problemが破綻)こと、複数のImage点電荷が数ないしは大きさについて収束しないと問題が閉じないことを指摘しました。各自でグラフ用紙に丁寧に作図して復習してみてください。演習で扱う問題3.35(p155)も同類の問題ですので注意深く解いてみてください。
(4)Image点電荷の置き方がほとんど自明と思われない例として、半径Rの(接地された)導体球の近くに点電荷qを置いた問題をp124Example3.2にそって考え始めました。適切な大きさのImage点電荷を適切な場所にたった1個置くだけでbounday conditionが満たされる点について、各自でcheckすることを宿題としたところで時間切れです。
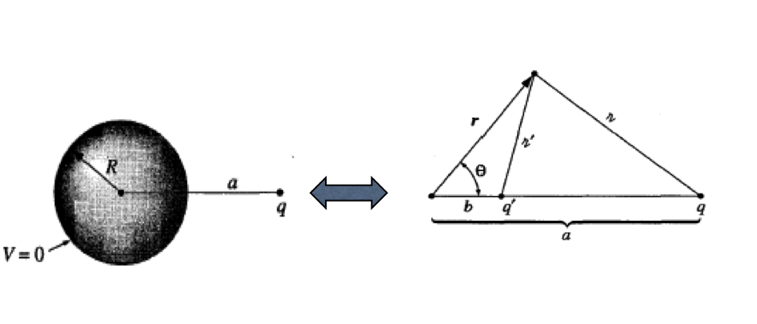
(5)次回は、Example3.2に関して課した計算check(どのような大きさのImage点電荷をどの場所に置くとbounday conditionが満たされるか?)を前提に話を始めます。この問題の数学的な裏打ちであるアポロニウスの円について余裕があれば見ておいてください。なお、Method of Imageは「ラプラス方程式の解の一意性」(テキストp116、3.1.5 Boundary Conditions and Uniqueness Theorems) に基づいた解法ですが、これについては次回に説明します。
10月17日(第4回目)の講義では
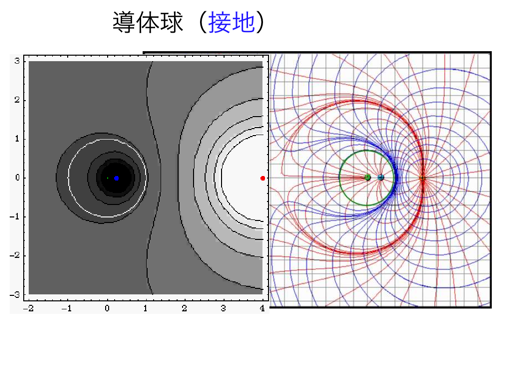
(1)Image点電荷の置き方がほとんど自明と思われない例として、半径Rの(接地された)導体球の近くに点電荷qを置いた問題をp124-Example3.2にそって説明しました。適切な大きさのImage点電荷を適切な場所にたった1個置くだけでbounday conditionが満たされた点はある意味驚きですが、数学的な裏打ちは(高校の数学で知っている)アポロニウスの円として知られる幾何にあります(導体球の表面が常に同じポテンシャル等位線に留まっている様をQuickTimeMovieでじっくり見てください)。
導体球の表面に誘起される電荷分布σ(θ)をNormal derivativeにより求めると、直感通り点電荷に最も近いθ=0で最大値をとり、対称軸まわりの回転角には依存しない、全電荷量がImage点電荷q’に等しいσ(θ)の表式が求まりました(Javaコンテンツ1(接地)を参照してください)。
この全電荷量が負の値を持つσ(θ)の電荷はどこから来たのでしょうか?導体球はもともと帯電していないはずです。
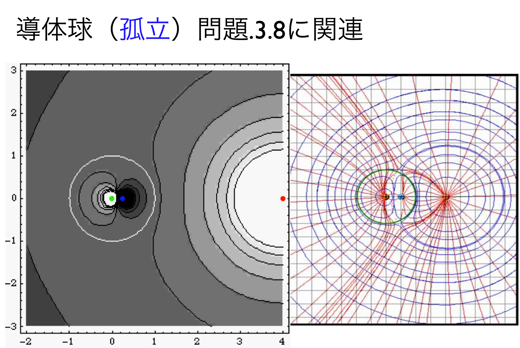
(2)同様に、半径Rの(孤立した)導体球の近くに点電荷qを置いた問題を考えました。先ほどの「(接地された)導体球の近くに点電荷qを置いた問題」において1個目のImage点電荷が置かれた事によりすでに球殻が同電位になっている状況をだいなしにすることなく、二つ目のImage点電荷(電荷量= - q’)を球の中心に置けば、球殻の全電荷量をゼロに保ち孤立系の条件を満たすことができます。
高電圧実験におけるアース(接地)の重要性を、最近研究室で強く実感した経験をまじえて、話しました。接地せずに(孤立した)導体球のポテンシャル値は、点電荷qを近づけるとどんどん上昇します。(導体球の表面が異なるポテンシャル等位線に飲み込まれて行く様をQuickTimeMovieでじっくり見てください)アース(接地)を取っていないと高電圧実験では思わぬ場所の電位が上昇し危険です。
導体球の表面に誘起される電荷分布σ(θ)をNormal derivativeにより求めると、直感通り、点電荷に最も近いθ=0で最大値をとる負の電荷分布を取りますが、裏側では正の電荷分布を持ち、その積分量である全電荷量がゼロに等しいσ(θ)の表式が求まりました。(Javaコンテンツ2(孤立)を参照してください)
(3)以上、説明した「(接地された)/(孤立した)導体球の近くに点電荷qを置いた問題」を対比させながら、誘導電荷分布σ(θ)の 接地/孤立での違い、球面上での電気力線の出入りの仕方の違い、球面上でのPotential値(ゼロ)/(点電荷の距離により変化する)の違いを、『電磁気学webコンテンツ集』の3章に置いてあるQuickTimeMovieを納得がいくまで見てください。
(4)この問題に関連してAssignment#7(後期2)として、半径RのGrounded hollow sphere内に中心点から距離aの場所に点電荷qがある時のPotential問題を出しました。この問題を解いて、method of imageの方法の理解を高めてください。
(5)「半径Rの(接地された)導体円柱棒の近くに平行に線電荷密度λの線電荷を置いた問題」を考えてみてください。2次元の問題で断面をみると、上述の導体球と同じで、アポロニウスの円の幾何は役に立ちそうですが、何が同じで、何が異なっているのか考えると、理解が進みます。
(5追記)Method of Imageは「ラプラス方程式の解の一意性」(テキストp116、3.1.5 Boundary Conditions and Uniqueness Theorems) に基づいた解法ですが、これについて、Direchet条件あるいはNeuman条件で与えられた境界条件を満足するが、領域内では異なるV1,V2を仮定すると、その結果として ∇(V1−V2)=0を導くことができ、よってV1=V2であり(細かいことを言えば、Neuman条件の場合は定数の差は未定)、解は一意的である事を示す論法で、説明をしました。
(6)p146の3.4 Multipole Expansion に進みました。
前期に、有限の電荷分布が作るポテンシャルV(r)の計算のcheckとして、十分遠方で「it looks like a point charge」を確かめて来ましたが、電荷分布の総量がゼロである場合には第0近似では(1/rの寄与をする)ポテンシャルはゼロであるが、電荷分布がある以上何かのポテンシャルはあるはずであるという問題意識を持って、+qとーqの点電荷が距離dだけ離れた電荷分布(電気双極子[Electric Dipole])を考え、十分遠方(r >> 電荷分布の広がりを表す長さ d)でポテンシャルV(r)を評価しました。QuickTimeMovieで見せた様に、r>>dの領域では、1個の点電荷の作るPotentialの示す1/r依存性より強い1/r^2のr依存性を持つこと、V(r)はその表式にあるCos(θ)の因子のため明らかなように等方的でないことがわかります。
(7)さらに、1/r^2のr依存性を持つ電気双極子を2個組み合わせた電荷分布(電気四重極子[Electric QuadruPole])では、QuickTimeMovieで見せた様に、1個の電気双極子の作るPotentialの示す1/r^2依存性より強い1/r^3のr依存性を持つこと、V(r)は電気双極子の場合より複雑な非等方性を示すことをがわかります。
(8)以上の導入を持って、任意の電荷分布ρ(r’)の作るポテンシャルを1/rのベキで表現するMultipole Expansion(多重極子展開)を、ルジャンドル多項式の母関数を利用して、議論し始めました。ここで時間切れです。
(9)次回は、Multipole Expansion(多重極子展開)の続きの話をして、p160の4章に入ります。
おまけ:Javaコンテンツ1&2は、物理学科の皆さんの5年ほど先輩の学部2年生当時の作品ですが、理科大を卒業後「理系のためのJava入門—「動く物理アプレット」でプレゼンテーション」という本を書いておられます。参考までに。
10月24日(第5回目)の講義では
(0)Assignment#7(後期#2)の解説をしました。
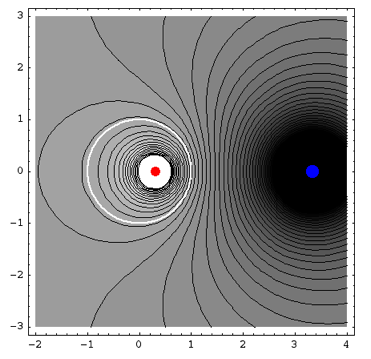
(1)任意の電荷分布ρ(r’)の作るポテンシャルを(原点からField Poinrまでの距離rの逆数である)1/rのベキで表現するMultipole Expansion(多重極子展開)の表式(p148の3.95式)からスタートして、n=0〜2の項を個別に見て行きました。
(i) n=0の項: 1/rの寄与をするMonopole項は全電荷が原点に集中したときの電気単極子(Electric Monopole) Q=スカラー による
(ii)n=1の項: 1/r2の寄与としてDipole項は電荷分布の原点のまわりでの偏りを表す電気双極子モーメント(Electric Dipole moment) P=ベクトル による
(iii)n=2の項: 1/r3の寄与としてQuadrupole項は電気4重極子モーメント(Electric Quadrupole moment)Qij=2階のテンソル による
ことを説明しました。
(2)特に、Quadrupole項については、問題3.45(p158)にあるような、直交座標系で2次形式で表されることを注意しておきました。
(3)Multipole Expansion(多重極子展開)を具体的に、原点からy方向にdだけ離れた位置に点電荷qを置いた電荷分布ρ(r')=qδ(x')δ(y'-d)δ(z')について用いてみました。この例では、多重極子展開において高次の項まで和を取ることにより初めてあらわになるポテンシャルの形が(実は)自明な(原点からy方向にdだけ離れた位置にある)点電荷ポテンシャルであるという答えがわかっているため、答えがわかっているポテンシャルからMonopole項を差し引いた残りが<主に>Dipole項で表せること、さらにDipole項を差し引くと残りが<主に>Quadrupole項で表現できることを味わうことができます。
図に出て来たMonopole項/Dipole項/Quadrupole項の解析的な表式を具体的に求めて、できれば各自で実際に(PC等を使って)作図してみると理解が深まると思います。
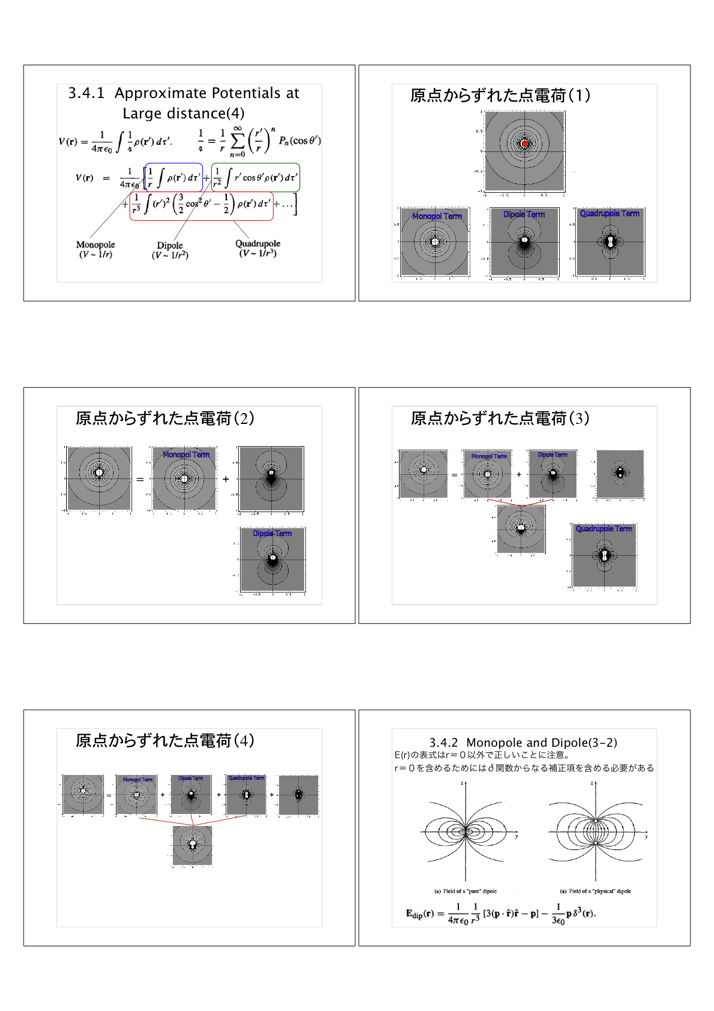
(4)Monopole項がゼロの場合はDipole moment(双極子)の値自身は原点の選び方によらず一意的にさだまるが、Monopole項がゼロでない場合はむしろ原点をうまく選ぶことによりDipole moment(双極子)をゼロにすることができることを強調しておきました。
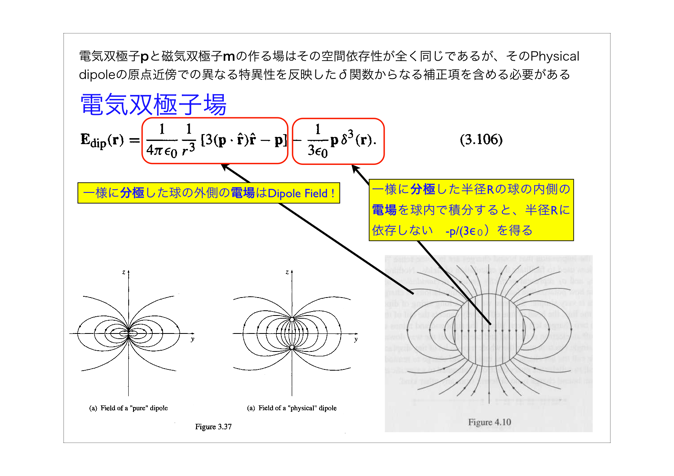
テキストで言及してある「Physical Dipole」と「Pure Dipole」の違いを強調しておきました。これについては磁気双極子モーメントの作る磁場をあとで扱う時に、水素原子の基底状態のエネルギー順位の超微細構造の話をする際にまたふれます。
(5)Dipole項によるポテンシャルV(r)の座標系によらない表式(p149の3.99式)のGradientを取り、公式(3)、(4)などを使いながら、Dipole項による電場E(r)を座標系によらない表式(p155の3.104式)で求める作業を各自でやってみましょう。
(6)p160の4章に入りました。これまでは電荷分布や電流を設定するために導体(Conductor)を考えて来ましたが、誘電体の登場です。 まず、誘電体という物質の構成要素である原子/分子が電場中に置かれると何が起こるか?を考えるために、水素原子を例に取り、一様な電場中で電気双極子がどのように誘起されるか?(atomic Polarizability α)について考えました。
(i)その最もPrimitiveな原子模型として一様球電荷分布(例題4.1)を考えα/4πε0=a0^3(a0はBohr半径)〜0.15 を得ました。電場中でも負の一様な球電荷分布は変わらないと仮定した点、誘起される電気双極子を計算するための原点は全電荷量がゼロなのでどこでも良いが、負の一様な球電荷分布の中心に取るのが簡単であった点を思い出してください。
(ii)量子力学の教えによる1S軌道の電荷分布(問題4.2)を考えα/4πε0=0.75a0^3(a0はBohr半径)〜0.09となり、電子分布の形が変わらないモデルでは実験値にほど遠いが、
(iii)2P軌道などの励起状態の波動関数が基底状態である1S軌道の波動関数に混ざることを反映した正確な量子力学的(摂動)計算を行うとα/4πε0=4.5 a0^3(a0はBohr半径)〜0.669となり非常に良く実験値を説明することを言及しました。量子力学の勉強が順調に進んでいればを1年半後にはこの話がわかるようになっています。
(7)次回は、p163の4.1.3 Alignmment of Polar Moleculesからテキスト順に話を進めて行きます。
10月31日(第6回目)の講義では
(1)4章にはいって、What happens to a piece of dielectric material when it is placed in an electric field?に答えるべく、誘電体という物質の構成要素である原子/分子が電場中に置かれると何が起こるか?を考え始めました。clear-cutではありませんが、大別するとneutral atom(non-polar molecules) の場合とpolar moleculesの場合で異なります。
先週扱った「一様な電場中での水素原子の分極」の例はneutral atom(non-polar molecules) の場合で、電場を加える前にはdipole momentが誘起されておらず電場を加えて初めてtiny dipole moment が電場の方向にinduceされましたが、 H2Oのようなpolar moleculesの場合はBuilt-Inのdipole momentが最初にありきで、それがN=P×Eなるtorqueを受け電場の方向を向くプロセスが有限温度での熱擾乱と競合し、平均として電場の方向にtiny dipole momentが向き、結果として、物質(誘電体)が分極(polarized)します。
(2)電気双極子Pが電場Eの中で、感じるポテンシャル U= -P・ E、受けるtorque N=P×E、電場の勾配により受ける並進の力 F=(P・ ∇)E(r) について、テキストより一般的に解説しました(エッセンスはテキストにある「ダンベル型のphysical dipole」で尽くされています)。 関連して、帯電した物体に(最初は帯電していない)紙切れがなぜ、引き寄せられるか?について、「電場の勾配により受ける並進の力 F=(P・ ∇)E(r)」を用いて説明しました。
「帯電した物体に(最初は帯電していない)紙切れがなぜ、引き寄せられるか?」に対する説明を簡潔に与えることをAssignment#8(後期#3)として設定しました。図と式を含む簡潔な(読んですぐにわかる)文章からなるレポートが要求されている基準です。
(3)原子スケールでは電荷分布は激しい空間変化を呈しますが、それを粗視化すると、セミマクロなスケールでは「単位体積あたりの電気双極子」(電気双極子密度)である分極P(r)(Plarization)は滑らかな空間変化を示し、これを電磁気学では扱います。分極P(r)(Plarization)により特徴づけられる物質(誘電体)が作り出す電場(ポテンシャル)を計算する際には、分極P(r)の存在と等価な[表面拘束電荷密度]σb(4.11式)と[体積拘束電荷密度]ρb(4.12式)を考えれば良いという話をしました。
(4)この等価性を実感するために、一様に分極した球の作るポテンシャルを、式4.9に従い直接積分する(p170問題4.12)方法と、分極P(r)の存在と等価な[拘束電荷密度]σb,ρbを用いて計算する(P168example4.2)方法で、実際に行い、確かに同じ答えになること示しました。 ここで時間切れです。
(5)次回はテキストにそって4.22(p170)から話を進めます。
(6)後期は2コマ目に授業があり終わるとお昼休みです。つまり、授業直後に質問があればそれに答える時間の余裕がありますので、どうぞ教卓付近に来てください(特別な会議がない限り、2コマ目が終わると直後には急務はありません)
もちろん、当日の内容でなくて以前の内容でも構いません(ただし、演習問題の「答えだけ」を教えてくださいは無しにしましょう)。
11月7日(第7回目)の講義では
(0)前回に解説したassignment#7「半径RのGrounded hollow sphere内に中心点から距離aの場所に点電荷qがある時のPotential問題をmethod of imageで考える」の補足として、「導体空洞の表面に誘起されるtotalの電荷量が点電荷qの位置によらず-qである」という積分結果(数学)の持つ物理的な意味を電気力線の持つ意味について立ち返り説明しました。assignment#8は先週説明した通りです。
(1)分極した物質が作り出す電場(ポテンシャル)を計算する際には、分極P(r)の存在と等価な[表面拘束電荷密度]σb(4.11式)と[体積拘束電荷密度]ρb(4.12式)を考えれば良いという話を、前回しましたが、これらの拘束電荷のオリジンをより明確にするために、例題4.3の説明をしました。 Example4.3が解説されている4.2.2 Physical Interpretation of bound charges (p170)を読んで、[拘束電荷密度]σb,ρbのイメージをとらえてみてください。
(2)もともと誘電体にある全電荷量はゼロですので、表面拘束電荷密度σbと体積拘束電荷密度ρbをすべて足し合わせるとゼロになるという点を強調しました。 (問題4.14(p173))
(3)物質(誘電体)の存在下ではガウスの法則(微分型)はどうなるか?の話をし、新しく D :electric displacement (名前は歴史的経緯によるもので、単なる補助量と考え、物理的な意味を考える必要がないというのが現代的な電磁気学テキストでの扱い方です)を導入し、自由電荷ρfだけで書かれたガウスの法則(微分型)が得られることを示しました。
(4)問題4.15をその具体例として2種類の方法(method1 & method2)で解きました。
(method1)σb,ρbを求めガウスの法則(積分型)を用いて電場Eを求める
(method2)electric displacement についてのガウスの法則(微分型)を用いて求める。
method2が断然速く解け、method2の有用性を示しました。
(5) method2が断然速く解けたので、その有効性をさらにcheckするため有限長のBar electret(問題4.17)についてmethod2を用いると、method1では納得できる結果になるにもかかわらず、どうもおかしな話(E=-P/ε0)?になってしました。これは∇・D=0から直ちにD=0と結論した点が間違っています。D=0と結論するためには∇×D=0も必要な条件ですが、∇×D=∇×Pとなり、高い対称性がないと一般には∇×P=0とはなりません。(問題4.15では球対称性のために、∇×P=0になっています)
(6)一様に分極した円柱(Bar Electoret)のどの場所で、∇×Pがゼロでない値をどの方向に取るか?を絵解きで考えました。 意外にもあたかも有限長のソレノイド電流により作られる磁場とのアナロジーが見えました。 各自でD,P,Eの場を定性的に描いてみて復習してみてください。
(7)Dについてのガウスの法則(微分型)を立てる際に、体積拘束電荷密度ρb=-∇・Pだけを∇・(ε0E+P)=ρfとして取り込みましたが、表面拘束電荷密度σbは考慮していませんでした。どうしてでしょうか?と質問を振りました。method1で、ガウスの法則(積分型)を使って問題を解く場合には実在する等価電荷としてσbも考えてます。 σbはρb=-∇・Pを誘電体表面で計量すると(界面で誘電体がなくなるのでヘビサイド型関数の微分であるデルタ関数的な取り扱いが必要ですが)すでに入っていることを注意しておきました。
(8)次回はテキストにしたがい、p179 4.4 Linear Dielectricsから話をします。
11月14日(第8回目)の講義では
p179 4.4 Linear Dielectricsから話を始めました。
(1)前回までは、Frozen-Inの電気分極Pを最初にありきとして、その効果(周りに作る電場(ポテンシャル)や等価な拘束電荷)を扱ってきましたが、ここでは、作用する電場に比例して分極が生じる線形誘電体を考えます。線形誘電体に関連して出て来た用語(electric susceptibility, permittivity, relative permittivity(dielectric constant)の説明をしました。真空の誘電率ε0という表現は真空があたかも誘電率ε0を持つある種の線形誘電体であるような印象を与えますが、ε0は単位系の選択により出て来たものに過ぎません。
(2)(線形)誘電体については電場EとElectric Displacement D の間にはD=εEという関係が生じますが、これがいかに『電場Eを求めるためには、分極Pから生じる拘束電荷分布を知る必要があり、分極Pを前もって知らなくてはいけない。しかしながら分極Pは電場Eをあらかじめ知らない限り計算できない』という連鎖を切断し問題解法に力を発揮しているか?をしっかり考えてください。
(3)それを実感できる例としてExample4.5[相当(設定が少し異なるが本質的には同じ)]の問題を解説しました。(この例でも球対称性のために∇×P=0になっていますので電気変位Dを電場Eと同等に扱って良い事になります)中空の中心に置かれた点電荷は誘電体に対して外場E0を与えているわけですが、誘電体自身が感じている場はE0だけでなく、自身が作り出した分極が作る電場も同時に見ていて、それらTotalの電場に対する応答として分極Pが起こっている点に注意してください。その意味で、この問題では、どのように『......』という連鎖を切断し問題解法に力を発揮しているか、言語化してみることを勧めます。また、この設定で見られた誘電体における部分的な静電遮蔽と、金属導体における完全な静電遮蔽誘とを、比較してみてください。
(4)p183に記述の「点電荷のまわりの全空間が(線形の)誘電体で満たされている例題」を用いて、設定した自由電荷分布ρfと比例関係にある相似形の拘束電荷分布ρbが誘起されることを解説しました。
(5)誘電体がある場合の電気映像法の例題として、左半面がε2、右半面がε1の誘電率を持つ誘電体で満たされているとき、境界面から距離dの右半面中に点電荷qを置いたときの、ポテンシャル(電場)を電気映像法により求めることを(4)で与えたことを前提に、考えてみてください。この例題はテキストにはありませんが、誘電体を含む電気映像法の典型例で多くの電磁気学のテキストで扱われています。
(6)テキスト4.4.3 Energy in Dielectric System に移り、誘電体の存在下で、電荷分布系のエネルギーをどう考えるかという話から始めました。 さきほど用いた例題4.5[相当]を再び登場させ、原点に少しずつ電荷を持ってきながら最終的に電荷Qを置いたとき、どれだけの仕事が必要か?を絵解きで説明し、[誘電体の存在下での全電荷分布(Free Charge と Bound Charge)の作る電場のエネルギー]と[誘電体の分極内に蓄えられた(バネのイメージを用いました) エネルギー]の2者からなることを説明しました。
(7)(線形)誘電体の存在下で電荷分布系が持つエネルギーの表式をテキストに準拠して導きました。エネルギーの表式(式4.58)は(線形)誘電体についてのみ成り立つ表式で、4章のはじめに出て来たFrozen-in Polarizationがありきの設定には使えません。誘電体の存在下でのエネルギーが、上述した2者からなることを定量的に示す例題として、原子の分極についてバネのモデルを用いた稀薄気体の例を話しました。
(8)テキスト4.4.4では(大学入試問題として良く出て来る)平行平板コンデンサーに誘電体をインサートした場合のエネルギーと働く力について解説していますが、来週休講なので、その間にWebにUpする資料( 2007-Nov-1,2,3 )によりその導出の計算をcheckしておいてほしい話(局在した電流分布が遠方に作るベクトルポテンシャルの多重極子展開)を先にすることにしました。
(9)それは、5 章で残っていた5.4.3 Mutipole Expansion of the Vector Potentialです。任意の局在した電荷分布が遠方に作る電位ポテンシャルを、ルジャンドル多項式の母関数を利用したMultipole Expansion(多重極子展開)で議論したように、一般的な局在した電流分布が遠方に作るベクトルポテンシャルも同様にルジャンドル多項式の母関数を利用したMultipole Expansion(多重極子展開)を用いて議論しますが、どのみち現段階では第2項目(磁気双極子)までしか考えないので、講義では、1/rのベキ展開をテーラー展開して話しました。 1/rの寄与は全電流の和がゼロであるためゼロになります。1/r2の寄与としてMagnetic Dipole(磁気双極子)からなる項を定義しました。 導出計算は補助プリントとしてwebにUPしてありますので( 2007-Nov-1,2,3 )各自で次回までに、読んでおいてください。
(10)次回は、飛ばした、テキスト4.4.4:平行平板コンデンサーに誘電体をインサートした場合のエネルギーと働く力について解説したのち、5.4.3 Mutipole Expansion of the Vector Potentialの残りの話をして、6章に入り、誘電体における分極Pの話と同様に、 磁化した物質(磁性体)の作る場について話します。
(11)次回の講義までにベクトル解析公式(問題1.60(b))を各自で復習しておいてください。
11月28日(第9回目)の講義では
(1)前回の授業後に問題4・23について質問があり、全体で共有すると良いと思いましたので、冒頭で解説をしました。
問題4・23は、球状の線形誘電体(電気感受率χ)が一様な外電場E0にさらされた時に誘電体内部の電場を逐次代入をして求める問題です。収束半径が保証されない場合に対しては、物理的には収斂値があるにもかかわらず、逐次代入の方法論自身が破綻していることが問題ですが、理解を深めるために、逐次代入ではなく、E0以外の最終的な分極による反電場Epについてのself-consistentな式を立てて考える方法を説明しました。self-consistentな式を解いて、答えである Ep=E0*(χ/3)/(1+(χ/3)) を出してみてください。
(2)4.4.4にある平行平板コンデンサーに誘電体をインサートした場合のエネルギーと働く力について話しました。誘電体が引き込まれるのはコンデンサー極板の端の電場(Fringing Field)が一様でなく勾配があるためですが、そういった詳細には触れないでもエネルギーバランスを考えることにより引き込む力の計算ができる点を強調しました。(同様な問題が、演習時間に扱う問題4.28にあります)
(3)(A)電荷Q-Fixedと(B)電位差V-Fixedに分けて話をし、(B)では電源がする仕事も勘定に入れないと誘電体が押し出される?間違った結論になってしまうことを説明しました。(A)(式4.64) と(B)(式4.67) で導かれる力は同じく引き込まれる引力ですが、同じx-依存性を持っているでしょうか?考えてみてください。
(4)5 章で残っていた5.4.3 Mutipole Expansion of the Vector Potential に戻りました。
一般的な局在した電流分布の作るベクトルポテンシャルを遠方で評価しました。テキストではルジャンドル多項式の母関数を利用したMultipole Expansion(多重極子展開)を用いていますが、第2項目までしか考えないので、講義では、1/rのベキ展開をテーラー展開して話しました。 1/rの寄与は全電流の和がゼロであるためゼロになります。1/r^2の寄与としてMagnetic Dipole(磁気双極子)からなる項を定義しました。 細かい導出計算は補助プリントをwebにUP( 2007-Nov-1,2,3 )してありますので各自で読んでおいてください。
(5)局在した電流分布の作るベクトルポテンシャルをMultipole Expansion(多重極子展開)した時、最初に顔を出す第二項目(1/r2の寄与)を担うMagnetic Dipole moment(磁気双極子 m)の意味するところをわかり易くするため、一般的な表式(5.91 式、p254)を電流 I を持つPlanar loop currentに適用して、磁気双極子 mが、どれだけの電流がどれだけの大きさの領域を回っているかで決まる量(5.84 式、p244)であることを見ました。
今年も言い忘れましたが、Multipole Expansion(多重極子展開)における第一項目を担うMagnetic Monopole moment(磁気単極子)が常にゼロであるため、Magnetic Dipole moment(磁気双極子 m)はその計算における原点に依存しません(Electric Dipole momentの場合と比較してみましょう:総電荷量がゼロでありelectric monpole がゼロである場合に限り電気双極子pはその計算における原点に依存しません)。
(6)Magnetic Dipole moment(磁気双極子 m)の作る磁場は、Electric Dipole moment(電気双極子 p)の作る電場と全く同じになることを強調しました。各自で、∇×A(dipole)を計算して、Coordinate-free form(5.87 式、p246)を導出してみましょう。
(7)磁気双極子mの作る磁場と電気双極子pの作る電場の空間分布が全く同じなのは、r=0以外のところに限られ、原点近傍での力線の振る舞いはmとpで異なることを絵解きでコメントしました。原点は特異点になっており、r=0についてはδ関数からなる新たな項が必要になります。この詳細については次週に話をします。水素原子は〜 -13.7 eVのエネルギーの基底状態を持ちますが、非常に小さいながら(エネルギー 〜0.000006 eV、振動数1422 M Hz, 波長21 cm)だけ分裂した「超微細構造(Hyperfine structure)」をもち、その説明にはこのδ関数からなる新たな項が必要になります。
(8)つぎに誘電体における分極Pの話と同様に、 磁化した物質(磁性体)はmagnetic dipole momentの密度である磁化M(r)(Magnetization)により特徴づけられ、磁化した物質が作り出す磁場(ベクトルポテンシャル)を計算する際には、磁化M(r)の存在と等価な表面拘束電流密度 K と体積拘束電流密度 J を考えれば良いという話を、誘電体における分極の場合と対比しながら話しました。磁性体におけるミクロなmagnetic dipole momentの成り立ちについては、来年の3年生向けの量子力学2や[後期]の物性論5で話があります。 具体的な導出はテキスト263-264を各自で読んできてください。
(9)次回は超微細構造(Hyperfine structure)を担う「磁気双極子mの作る磁場の表式におけるδ関数項」の話をして、p264以降テキストにそって話をします。
12月5日(第10回目)の講義では
(1)p263 6.2.1 Bound Currentsからテキストに沿って話をしました。誘電体における分極Pの話と同様に、 磁化した物質(磁性体)はmagnetic dipole momentの密度である磁化M(r)(Magnetization)により特徴づけられ、磁化した物質が作り出す磁場(ベクトルポテンシャル)を計算する際には、磁化M(r)の存在と等価な表面拘束電流密度 Kb と体積拘束電流密度 Jb を考えれば良いという話を、誘電体における分極の場合と対比しながら話しました。磁性体におけるミクロなmagnetic dipole momentの成り立ちについては、来年の3年生向けの量子力学2や[後期]の物性論5で話があります。
(2)この拘束電流J&Kの表式を用いて問題6.7&6.8の設定におけるJ&Kを実際に計算してみました。 問題6.8では拘束電流J&Kの総和がゼロになっていましたが、「誘電体の拘束電荷について確かめた総和則(問題4.14:全電荷量はもともとゼロ!)」と同様に、磁性体における拘束電流についても総和則が成り立っていることを話しました。
(3)数学的導出で求めたJ&Kの表式ではその物理的な意味付けがはっきりしませんので、テキストに従いそれを与えました。ミクロなmagnetic dipole momentを担っているミクロなLoop電流がどのようにCancelしないかによりマクロな電流 Jb=∇×M & Kb=M×n が生き残ります。
(4)テキストp269 6.3 The Auxiliary Field H に進みました。 誘電体で補助場Dを導入したのと同様に、磁性体では補助場Hを導入すると拘束電流から解放されてfreeCurrent(自由電流/真電流)だけを考えれば良いアンペールの法則(微分型)∇・H =Jfreeが得られます。問題6.8&6.9について、『拘束電流J&Kを求めアンペールの法則(積分型)を用いて磁場Bを求める(方法1)』と『H についてのアンペールの法則(微分型)を用いて求める(方法2)』を用いてみましたが、方法2が断然速く解けることを示しました。これは、誘電体でした話と同じ話です。
(4’)磁場Bの名前について、Bは「磁束密度(magnetic flux density)」で「磁場の強さ」Hと区別するよう高等学校でならったと思いますが、現代的なの電磁気学のテキストにおいては『Bを単純に磁場(magnetic field)と呼び、磁性体を含む静磁気学を論ずる際に導入した H は名前を付けず、ただHと呼ぶ』というコンセンサスがあるという話を補足しておきました。
(5)しかしながら、方法2は無限長のBar Magnetについては確かにうまく行きましたが、有限長のBar Magnetについては、どうもおかしな話になってしまうがどうしてか?を発問して時間切れです。
(6)次回は6.3.2 A Deceptive Parallelから話を進め、予告しておいた「水素原子における超微細構造(Hyperfine structure)を担う「磁気双極子mの作る磁場の表式におけるδ関数項」」の話をします。有限長のBar Magnet(磁性体)の例題を各自で考えておいてください。
12月12日(第11回目)の講義では
(1)6.3.2 A Deceptive Parallelから話を進めました。先週、Frozen-Inの磁化分布M(r)が作る磁場分布B(r)を求める方法として、『拘束電流J&Kを求めアンペールの法則(積分型)を用いて磁場Bを求める(方法1)と『H についてのアンペールの法則(微分型)を用いて求める(方法2)』について話し、(方法2)は無限長のBar Magnetについては確かにうまく行くが、有限長のBar Magnetについてはどうもおかしな話になってしまうがどうしてか?を発問しました。この例題でわかるように、補助場Hに対する場の方程式(∇×H=Jfree)を見て補助場Hを磁場Bと平行に扱って良いと思ってはいけません。この例では円柱の上端&下端面で∇・H= -∇・M≠0でした。 (∇・B=0は常に成り立っています)
(2)円柱軸方向に一様に磁化した有限長のBar Magnet(磁性体)と円柱軸方向に一様に分極した有限長のBar electret(誘電体)をパラレルに扱い、
Hには等価磁荷( -∇・M)
Bには等価電流(∇×M)
Eには等価電荷(-∇・P)
Dには 等価磁流(∇×P)
の助けを借りて作図しました。等価磁流(∇×P)という言葉はテキストでは見かけませんが、前期に話した『もしMagnetic monopole(磁気単極子:磁荷)があれば、∇・Bの右辺にそれが現れ、磁荷の流れに対応する磁流が∇×Eの右辺に現れ、静電場と静磁場は全く対称になること』を思い出して、その対応を考えてください。
(3)また、これらH、B、E、Dの力線の形を見ながら相違点と類似点は何か? を良く考えてください。作図で力線を正確に描くためには、H、B、E、Dに関する境界条件を意識する必要があります。くどいかもしれませんが、この例では
Eについては、表面電荷密度分布σ(ここでは等価電荷(-∇・P))がある場合は、電場EのNormal 成分はσ/ε0の飛びがあり不連続である(式4.28)一方、Tangential成分は連続である(式4.29)。
Dについては、表面電荷密度分布σがない場合は、DのNormal 成分は連続である(式4.26)一方、Tangential成分は等価磁流(∇×P)があるため不連続である(式4.27)。
Bについては、表面電流密度分布K(ここでは等価電流(∇×M))がある場合は、磁場BのNormal 成分は連続である(式5.72)一方、Tangential成分はKμ0の飛びがあり不連続である(式5.73)
Hについては、表面電流密度分布Kがない場合は、HのTangential成分は連続である(式6.25)一方、Normal 成分は等価磁荷( -∇・M)があるため不連続である(式6.24)。
に注意すると、境界条件の意味と必要性がわかると思います。
(4)講義では言い忘れましたが、誘電体で、Dについてのガウスの法則(微分型)を立てる際に、体積拘束電荷密度ρbを-∇・Pとして∇・(ε0E+P)=ρfの形で取り込んでも表面拘束電荷密度σbを考慮していなかったことと同様に、磁性体で補助場Hについてのアンペールの法則(微分型)を立てる際に、体積拘束電流Jbを∇×Mとして∇×(B/μ0 - M)=Jfの形で取り込んでも表面拘束電流Kbを考慮していませんが、KbはJb=∇×Mを磁性体表面で計量する際にすでに入っている事情は表面拘束電荷密度σbと同じことを指摘しておきます。
(5)電気感受率χeがEに対するPの応答の仕方として定義されたことに対応して、磁気感受率χmもBに対するMの応答の仕方として定義されるように思えますが、実験室でコイルを流れるfree currentを制御してHを制御しその結果、コイル内の物質の磁化Mが決まりBが定まる状況では、習慣として、磁気感受率χmはHに対するMの応答の仕方として定義される点を説明しました(コンデンサーでfree chargeを制御するわけではなく、極板間の電位差を電源で制御してDではなくEを制御している点に注意してください:テキストp271にある As it turns out, H is a more .... Just call it H! を熟読してみましょう) 。
(6)次回(後期 第12回目)は12/15の補講の時間帯です。
(i)予告しておいた「水素原子における超微細構造(Hyperfine structure)を担う「磁気双極子mの作る磁場の表式におけるδ関数項」」の話、
(ii)MITオープンコースWareの動画を見ながら強磁性体の話(p278 6.4.2 Ferromagnetism)、
(iii)電磁場と相対論の関係についての導入的な話
をします。
(7)
(i) 12/19(後期 第13回目)は予告通りテストをしますので、学生証を忘れずに持って来てください。10:30にはスタートできるよう時間厳守でお願します。
(ii)12/22 (後期 第14回目)は補講の時間帯です。
12月15日(第12回目)の講義では
(1)Maxwell方程式(7.42式)を見ると、電場と磁場は電荷と電流をその源(Source)として持ち、さらに相互の時間変化(Maxwell項、ファラデー項)を加えて場が作られると読めますが、電場と磁場は絶対的なものではありません。たとえは十分ではありませんが、人間の顔のようなもので、正面と側面では、一つの実体である「人間の顔」が異なる見え方をします。電場、磁場も絶対的な意味を持つ訳ではなく、電磁場という一つの実体の異なる見え方であると言えます。それらを体感してもらうために、簡単な例を用いて、電磁場と相対論の関係についての導入的な話をしました。F系とF’系で座標系を変えると、電場、磁場の現れ方、および、場の源である表面電荷密度と表面電流は大きく変わりました。しかしその結果は、『F系とF’系で座標系を変えても、点電荷に力が作用せず加速度運動をしていないという物理的状況は同じである』ということと整合するものでした。(Maxwell方程式はローレンツ共変性を持ちます)既に相対論の講義でこの点についても話を聞いているかと思いますが、是非、12章(p477〜)特に、p522 の 12.3 Reativistic electrodynamicsを読んで、「Deep undestanding of the structure of electrodynamics」を味わってほしいと思います。 その際には、電磁気マテリアル集の「12 Electrodynamics and Relativity (電気力学と相対論)」が未完ですが参考になると思います。
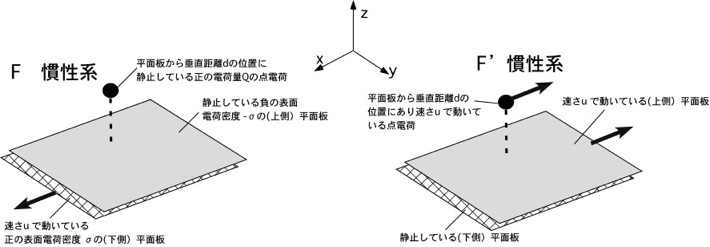
この図は2006年度後期の試験問題に用いたもので、講義で話した例と異なり、F系における電荷密度の正負が逆に設定してありますので注意を。
(2)MITオープンコースWareの動画を見ながら強磁性体(p278 6.4.2 Ferromagnetism)に関連する話をしました。
Barkhausen effectの話から始めました。
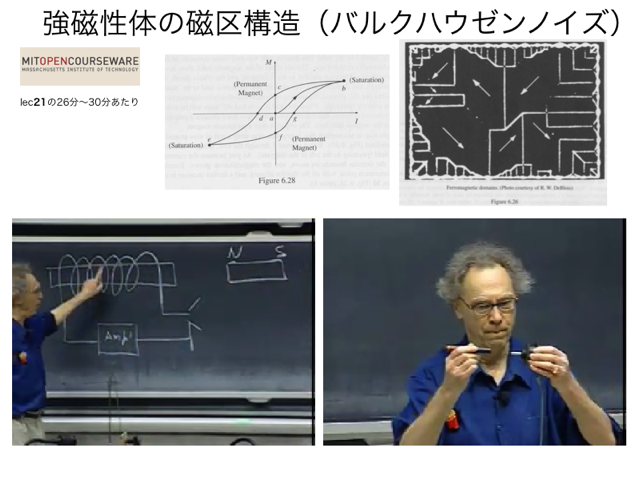
強磁性体の磁化過程におけるヒステリシスと交流消磁については時間の都合で見せませんでしたが、一応載せておきます。
交流消磁は3B学生実験課題「VSM磁化測定」の超伝導体のマイスナー効果の実験で必要な手続きとして触れることができます。

電磁石の設計では大事な磁気回路に関係するデモを見ました。
室温で強磁性を示す鉄もキューリー温度以上ではその強磁性を失います。この磁気相転移現象は、3B学生実験課題「磁性体の計算機シミュレーション」、3B学生実験課題「強磁性体の磁化測定」、3B学生実験課題「VSM磁化測定」で体感できます。

酸素分子は不対電子を持つため常磁性を示します(強磁性体ではありません)

(3)先延ばしになっていましたが、水素原子における超微細構造(Hyperfine structure)を担う「磁気双極子mの作る磁場の表式におけるδ関数項」の話をしました。時間がなかったので説明が荒くなってしまいましたが、磁気モーメントの大きさを一定に保ったままLoop電流の半径をゼロにする極限を取る操作には困難がありますが、1方向に一様に磁化した球の外部に作る磁場がまさに問題にしている磁気双極子場であることに気が付けば、磁気モーメントの大きさを一定に保ったまま、球の半径をゼロにする点極限を取ることは容易であることがポイントです。

量子力学の学習が進んでいる1年後に、水素の1s 基底状態の波動関数が原点で有限の値を持つ意味を、「磁気双極子mの作る磁場の表式におけるδ関数項」の話を思い出して、水素原子における超微細構造(Hyperfine structure)で実感してください。
(4)次回12/19(後期 第13回目)は予告通りテストをしますので、学生証を忘れずに持って来てください。10:30にはスタートできるよう時間厳守でお願します。
12月19日(第13回目)の講義では
60 分程度の時間を使ってテストを行ないました。時間が不足であると意思表示した人が大多数だったので、10:35〜11:55 netで80分のテストを行ないました。


12月22日(第14回目)の講義では
(1)問題の解説をしました。
(2)7章に戻り、誘電体&磁性体の存在下でのMaxwell方程式(7.55式)を足早に導出しました。誘電体&磁性体の存在下での静電場、静磁場を考えた際に導入した分極電荷(-∇・P)、磁化電流(∇×M)に加え、新たにSourceとして加わったのは分極電荷の時間変化にともなう電流(分極電流polarization current)です。
(3)本来は、ここからテキストp375に進み、電磁波の話をする予定でしたが、(1)に時間をとられて、ここで終わりです。一年間ご苦労様でした。
(4)後期の定期試験(1/23の予定)については授業(12/22)で話した通りです。
任意提出のeMailレポートの締め切りは年内(12/31の23:59:JSTまで)です。その趣旨は授業で話した通りです。講義内容のどういった理解をどこまで確かめるかを明確にした問題のデザインは、かなりの難問です(単純に「...を論ぜよ、......を説明せよ」は問題としては成立しません)。提出すれば単純に成績評価に加味される類のレポートではありませんので、誤解のないようにお願します。
授業(12/22)で話した通り、作成した問題とともに、「講義内容のどういった理解をどこまで確かめるのか?」という問題設計の意図について自身の言葉で述べてください(問題自身から何を問いたいかは十分想像できますが、問題設計の意図についての自身の言葉による説明も任意提出のeMailレポートのなかで大きく評価したい点です)。
送り先のメールアドレスは
任意提出のeMailレポートについて
約40人のひとから「講義内容のどういった理解をどこまで確かめるかを明確にした問題のデザイン」の任意提出のeMailレポートを受け取りました。
(1)取り組みの度合いに応じた評価を「任意提出のeMailレポート」について行い、それを総合成績評価に加算します。
(2)後期定期テストの問題自身は、eMailレポートで提案された問題ズバリそのものではありませんが、提案された問題のエッセンスをできるだけ多く反映させました。(提案された問題でそのエッセンスが取り入れられていない「良い問題」もありますが、それは(1)で取り入られていると理解してください)
後期の定期試験(1/23の予定)について
(3)最初はテキスト持ち込み可にしようと考えていましたが、ベクトル解析公式など煩雑な表式を記憶しておく必要のない(必要ならば問題文で与える)問題を出すので、筆記用具以外は一切持ち込み不可とします。
(4)試験範囲は授業で扱った後期の内容です(後期の内容は前期の内容の上に積み上げられたものですので必然的に前期の内容も前提になります:Maxwell方程式は書ける様にしておいてください):ただし12/15に話した「相対論と電磁気学の関係」は範囲から外します。
2007年度の成績評価を7F物理事務室前の掲示板に張り出しました。
総合得点 160点満点 = 前期定期試験(40/115) + 中間試験(40/105)+ 後期定期試験(40/105)+ アサインメント(40/645)
で算出しました。なお、年末の問題作成レポートをメール提出し、満田からの「受け取りのメール」を受け取った人には3点加点しました。
(判定が変わる D->C , C->B, B->A場合のみ、張り出した成績評価に明示しました)
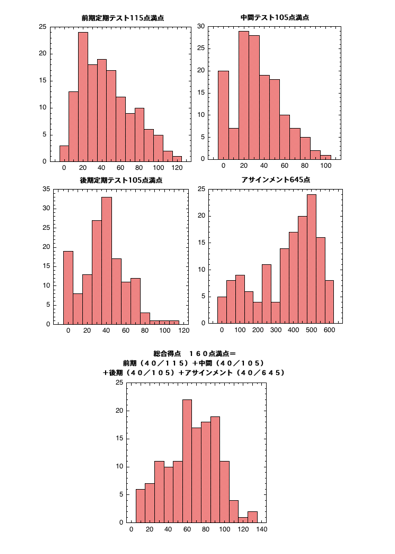
個々のテストで満点近くの点数を取っている人が必ずいますので、問題の難易度は適切であると考えています。
すべてを加えた満点は160点になるような算出をしていますので、合格/不合格の境界値である60点は何とか取ってほしいと思います。
58点と60点のどこが違うのか?と思う人がいるかと思いますが、基準を設定すると必ずどこかで合格/不合格の境界値が定まります。十分クリアーできる(してほしい)境界値になるような算出をしていますので、納得をしてください。(ミスは無いとは言えませんので、自身が持っているテストの出来の印象と著しく異なる場合は、至急、満田までコンタクトしてください。)