4 月17日(第1回目)の講義
4 月24日(第2回目)の講義
5 月 1日(第3回目)の講義
5 月 8日(第4回目)の講義
5 月15日(第5回目)の講義
5 月22日(第6回目)の講義
5 月29日(第7回目)の講義
6 月 5 日(第8回目) の講義
6 月12日(第9回目) の講義
6 月19日(第10回目) の講義
6 月26日(第11回目) の講義
7月 3日(第12回目) の講義
7月10日(第13回目) の講義
7月14日(第14回目) の講義
4月17日(第1回目)の講義では
(1)Assignmentの目的とその進め方、講義の範囲とその進め方について導入的な話をしました。Face to Faceの対面授業の効果を高めるためには学生の皆さんの「共同作業としての授業へのparticipation」が重要であるという話をしましたが、是非、その意識を持って授業に出てください。
(2)これから用いる表記の紹介を兼ねて、(1年生の学生実験で実際に体感した)クーロンの法則の復習から始めました。

source charge, test charge, source point, field pointなど用語がいろいろ出て来ましたが、きちんと定着させてください。言い忘れましたが、クーロンの法則はsource chargeが静止している場合に成り立つ法則(test chargeは動いていても良い)です。source charge(点電荷)が速度vで動いている場合は、電場の様を表す電気力線はもはや等方的でなく、p440(図10.10)にあるように速度ベクトルvと垂直方向に密になります(このあたりは3年生の電気力学で学習することになります)
(3)電気力についてのクーロンの法則と同じく距離の逆二乗則を示すものとして重力があります。電気力には正、負の二種類の電荷がありますが、質量には正、負はありません。この似て非なる二つの法則の違いを理解するために、Assignmnet#1(問題1)を出しました。
(4)連続的な電荷分布の場合は、電場の表式は(p62の式2.8)
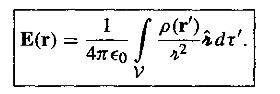
で与えられ(このテキストでは、この表式をしばしば「クーロンの法則」として言及しています。また、そこで用いられている『重ね合わせの原理』は自明ではなく実験事実であること(p58 footNote1を参照)を強調しました。)、差分単位位置ベクトル(筆記体(授業では花文字アールと呼びます)アールーハット?)は積分中に向きが動くこと(p62 footNote2を参照)を注意し、具体例として問題2.6を解説しました。
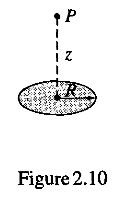
ベクトル的足し合わせの結果、被積分関数にCos(θ)をかける必要があること(θはz軸と筆記体アールーハット?の成す角度)を説明しました。z=0の場合はどうなるか?各自で考えて見てください。
(5)問題2.6を解いて出てきた表式を(Z >> R)で漸近評価し、有限の大きさを持つ電荷分布は十分離れれば点電荷として振る舞うことを強調しました。これは 有限の大きさを持つ電荷分布に対しては(無限に広い面電荷分布、無限に長い線電荷分布は除きます)いつも成り立つ話ですので、ある(有限の)電荷分布を計算したとき、その計算がおかしくないか?をcheckする方法になることを強調しておきました。
(6)連続的な電荷分布の作る電場の計算(微小電荷要素のつくる電場のベクトル的足し合わせによる)の同様な例として、問題2.7をAssignment#1(問題2)に指定しました。
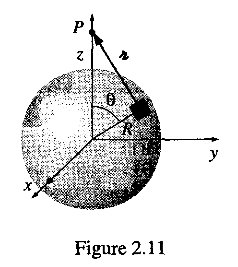
これらの答えは1年生の物理学でガウスの法則を用いて計算したことがあると思いますが、ガウスの法則を使わずに積分(式2.8)で計算してください。
(7)次回はAssignment#1の解説をして、問題2.8を解き、p65以降の「ガウスの法則」「電場のDivergence & Curl」について話を進めます。
4月24日(第2回目)の講義では
(1)Assignment#1の解説をしました。問題1を通して電気力が大きい力であること、日常生活の中でその大きさを直接感じない理由が、わかったと思います。問題2(2.7(球殻電荷分布))は、連続的な電荷分布の作る電場の計算(微小電荷要素のつくる電場のベクトル的足し合わせによる)の典型的な例題ですが、
(i)「球殻の外側ではあたかも原点に全電荷が集中しているがごとく見なせる電場が作られること」、
(ii)「球殻の内側では電場はどこでもゼロになること」、
(iii)「z=Rでは球殻の半径の大きさに依存せず、σ/ε0のジャンプがあること」
を言及しました。
(2)z=Rでの電場を計算すると、内側の0と外側のσ/ε0の平均であるσ/2ε0であることを述べましたが、これ自身、極最近の「大学の物理教育」誌で話題になっていた話
Vol.12-2(2006年7月) 講義室 ガウスの法則やアンペールの法則を教えていて気になること
Vol.12-3(2006年11月) 講義室 金属球殻表面の電場
講義室 ガウスの法則補遺 —田中氏の論文に対するコメント—
Vol.13-1(2007年3月)講義室 球面上の電場は定義すべきか)
ですので少し後になってからでも雑誌「大学の物理教育」を読む機会があれば読んでみてください。前回扱った問題2.6のz=0では電場は不定ではなくゼロ!です。
(3)同様に、問題2.8を取り上げましたが、極座標で3重積分をあらためて計算しなくても問題2.7の結果を用いて結果が出せることを被積分関数を図解して説明しました。
(4)問題2.7 で得られた「球殻の内側では電場はどこでもゼロになる」という結果をより定性的に理解できるように、「立体角(Solid Angle)を用いた議論」で説明しました。ここでは見込む電荷量の違いが、距離の違いを補っていることと、球形ゆえCos(ψ)の射影因子が共通であることがポイントであることを指摘しておきました。また「球殻の内側では電場はどこでもゼロになる」性質は、高い精度でクーロンの法則を実験的に検証することに利用できることを言及しました(詳細は、2.5 Conductors(導体)で話します)
(5)微小電荷要素のつくる電場のベクトル的足し合わせによることなく、場を計算するパワフルなガウスの法則は既に、1年生の物理学で(立体角(Solid Angle)を用いた議論により)学習していますが、ここでは、「ガウスの法則(物理法則)」=ガウスの発散定理(数学定理)+クーロンの法則(物理法則)の成り立ちに基づき説明しました。

授業中にはっきり言うのを忘れましたが、この式2.13で表されるガウスの法則は積分形で書かれているので「ガウスの法則(積分型)」と呼ばれます。
(6)問題2.12(p75)を取り上げ、球電荷分布の作る電場を「ガウスの法則」(積分型)で求める話をしました。
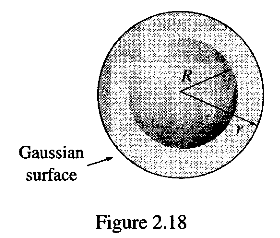
(7)例題2.6(p73)を取り上げ、帯電した無限に広い平面版の作る電場を「ガウスの法則」(積分型)で求める話をしました。大きさが、平面からの距離によらずσ/2ε0である電場は、前回扱った問題2.6の解をz=有限、R->無限大で漸近評価したものと一致します。
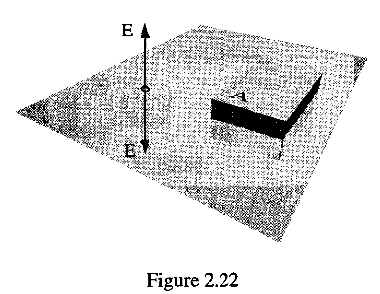
(8)問題2.13(p75)を取り上げ、無限に長い線電荷分布の作る電場を「ガウスの法則」(積分型)で求める話をました。
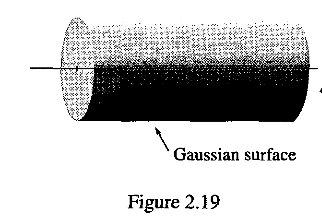
(9)「ガウスの法則」(積分型)を用いる際に、電荷分布の持つ空間対称性から電場の満たすべき空間対称性を如何に引き出すか?がポイントになります。与えられた電荷分布について、微小電荷要素のつくる電場のベクトル的足し合わせを目で大雑把に行って電場の当たりをつけるのではなく、電荷分布の持つ空間対称性から電場の満たすべき空間対称性を見出してください。
(10)「ガウスの法則」は常に正しいが、usefullなのは電荷分布の持つ高い空間対称性に起因する電場の呈する空間対称性があるときだけで、Spherical/Cylndrical/Plane Symmetry に限られることを話しました。example2.5(p74)のように全体ではそれらの対称性を持たないが、対称性を有するObjectに分解できる場合は分解したObjectについて「ガウスの法則」を適用し、重ね合わせの原理を用いればよい話をし、その良い例題として、問題2.18(2個の球電荷だんご?)をassignment#2の一つとして予約しました。(その後、assignment#2ではなく、後期のassignment#??で出すことに変更しました)
(11)次回は静電場Eを記述する場の方程式∇×E=0、∇・E=ρ/ε0を求める話から始め、p77以降のPotentialに進みます。ベクトル解析の怪しい人は、p53の1.6.2のPotentialsを読んでおいてください。(irrotational fieldの持つ性質について)
(12)授業の途中でも、直後でも、質問したいことがあれば気軽に質問してください。
5月1日(第3回目)の講義では
(1)静電場Eというベクトル場を記述するためには、(ヘルムホルツの定理(p555)にあるように)そのDivergenceとRotationを知る必要があります。広義のクーロンの法則(式2.8)の表式からスタートして、そのDivergenceとRotationを求めることにより、静電場Eを記述する場の方程式 ∇×E=0、∇・E=ρ/ε0 を得ました。授業中にはっきり言うのを忘れましたが、 ∇・E=ρ/ε0 は、いわばガウスの法則を微分形で書かれているので「ガウスの法則(微分型)」と呼ばれます。
Divergenceについては逆二乗則の持つ特異性(原点ではデルタ関数型の特異性があるがそれ以外はすべてゼロ)がポイントで、∇・E=ρ/ε0なる場の方程式が得られました。
Rotationについては動径方向を向くベクトル場であるため、すべてゼロになり、∇×E=0なる場の方程式が得られました。ただし、Divergenceで見られたような原点での特異性がないことを、問題1.60(b)の数学定理を用いて確かめておきました。
(2)Electric potential V(r) (電気ポテンシャル、電位)を2.29式で導入し、
(i)電場が『Derivable from a potential』であること、
(ii)名前がpotentialエネルギーと紛らわしいこと(単位はボルト!)、
(iii) 電場ベクトルの3成分は∇×E=0で表される強い関連があり、3成分は独立でないゆえ、Electric potential V(r) では1成分のスカラーで表現され 、電場の重ね合わせではベクトル和を扱うのに対してElectric potential V(r)はスカラー和を扱い簡単であり、Advantageがあることを言及しました。
Electric potential V(r)の意味を知るため、電場に抗して単位正電荷を運ぶ仕事を考え、電場がガウスの法則等で予め求まっているときは式2.21により任意の経路で線積分してpotentialを求めることができることを説明しました(経路の任意性は、∇×E=0の場はirrotational field(渦なし場)でありConservative Field(保存場)であることに起因します。ベクトル解析で学習したことを思い出してください)。Electric potential V(r)の通常の基準点の選択は無限遠方でpotential=0としますが、無限長線電荷分布や無限平面電荷分布には当てはまらないことを説明しました。テキストp80で基準点の選択に関してnatural spotについての記述がありますので読んでみましょう。

なおElectric potential V(r)
を体感するための実験は既に学生実験1の電磁気学関連題目群の中にある「静電場の性質」があります。既に忘れてしまっているかと思いますが、「静電場の性質」をweb上で見てV(r)
が「重ね合わせの原理」に従うこと、点電荷が示す 1/r 距離依存性が見えると思っていたら、線電荷分布が示す log(r)
距離依存性が実験的に求まったことなどを思い出してください。
(3)assignment#2(問題1)として、一様に帯電した半径Rの球(全電荷量はqとする)のポテンシャルの表式V(r)を二つの方法(式2.21および式2.29を用いる方法)で求める問題を出しました。
assignment#2(問題2)は距離の逆二乗則を持つ場を考える際に有効な「立体角の理解」を問う問題を出しました。
(4)p87 Fig2.35にある「電荷分布ρ」vs「電場 E」vs「Potential V」の関係を、これまで学習した事項の整理として、説明しました。
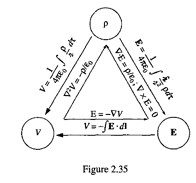
『Potential -> 電荷分布
』に出てくるPotentialというスカラー場が満たす場の方程式(名前は言い忘れましたが、Laplace方程式∇^2V(r)=0)については、物理数学2で学習する偏微分方程式における境界値問題として、後期にChapter3で話します。物理数学2の内容が難しいと感じている人が多いようですが、後期からは物理数学2で学習した内容も使い始めるので、頑張って咀嚼してください。
(5)次回は、問題2.25(a)(p86)の解説をから始めて、表面電荷分布によるσ/ε0の電場の飛びの話(p88〜)をして、p90の静電場のエネルギーに進みます。
5月8日(第4回目)の講義では
(0)Assignment#2の問題1の解説をしました。
問題1の(i)は、基準点を無限に取り、経路を動径方向にそった直線で考えました。field pointが球分布の外の場合(r>R)は、無限遠方からrまでの区間にわたり、被積分関数~1/(r’^2) について積分をすれば良い訳ですが、field pointが球分布の内側の場合(R>r)は、積分が、(無限遠方からRまでの積分区間にわたる被積分関数~1/(r’^2) についての)積分と、(Rからrまでの積分区間にわたる被積分関数~r ’についての)積分の和となることに注意してください。
問題1の(ii)は極座標(r、θ、φ)を用いて電荷分布にわたり積分しますが、θ、φの積分を終えてrについての積分をする際に、その被積分関数が、(r’< z)と(r’ > z)で異なること、よってfield pointが球分布の内側(R>z)の場合は r についての積分を(0〜z)の区間と(z〜R)の区間に分けて行う必要があることに注意してください。field pointが球分布の外側(z>R)の場合は積分区間を区切ること無く(0〜R)の区間で積分すれば良いことになります。
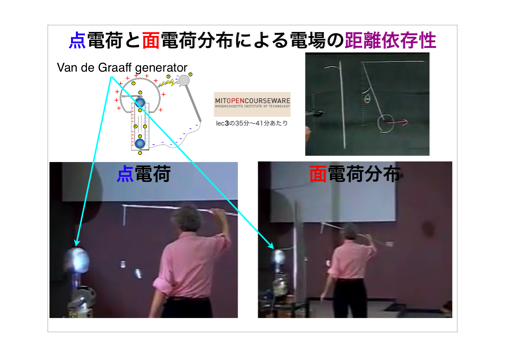
(1)MITオープンコースウエア(Physics:8-02Electricity-and-MagnetismSpring2002)のビデオlecture
http://ocw.mit.edu/OcwWeb/Physics/8-02Electricity-and-MagnetismSpring2002/VideoLectures/index.htmから
「Electric Potentialを体感するデモ実験」(wl-802-lec4-220k.rm の 45:00〜最後の部分)と
「点電荷と面電荷分布による電場の距離依存性を体感するデモ実験」(wl-802-lec3-220k.rm の 35:00〜40:00の部分)
を見てもらいました。
最初にこのビデオlectureを見た時は、丁度、「(NIME)研修講座[平成16年度]フレキシブルラーニング環境における授業づくり」という授業改善のFD研修を受けていた時期で、そのときの報告書に
「MIT オープンコースウエアにある電磁気学のVideo Lecture(8) では、独特の個性を放つProf. Walter Lewin氏が初等電磁気学について演示実験を混ぜながら半期にわたり行った講義をビデオ収録したものをストリーミング配信で見る事ができるが、非常に面白い!の一言に尽きる。演示実験が持つライブ感がこの講義を魅力的にしているのは確かであるが、知識伝達にとどまらない「物理の香り?」のようなものが流れていると感じる。」
と書いていましたが、今でも良く出来たマテリアルだという印象は変わりません。Real 形式でストリーミング配信していますので、時間のあるときに、是非見てください。

(2)Assignment#2の問題2の解説をしました。
ガウスの法則の証明にも有効だった立体角がなぜ有効であったか?再認識できたのではないかと思います。
(3)Assignment#2は1週間後の5/15〜16を目標にTAの人がマークングして返却しますので質問受け付け(金曜日 夜間3-4時限(17:50-19:20) 1138 教室)は5/18になる予定です(決まれば、物理学科Web掲示板で伝達します)ので、是非、TAによる質問受付を有効活用してください。もちろん、本日の様に、授業中の質問は歓迎します。(来週の授業まで明日から出張ですぐには時間が取れませんが、web質問箱のようなものを考えてみます)
(4)表面電荷分布を持つ具体例(問題2.6/問題2.7)で表面電荷分布の詳細によらず、σ/ε0の電場の飛びがあることに気がついていたと思いますが、その一般論をテキスト(p88〜90)に従い、表面電荷密度分布がある場合は、電場のNormal 成分はσ/ε0の飛びがある一方Tangential成分は連続であることを説明しました。

(5)点電荷分布に蓄えられるエネルギーについて、「The energy of a point charge distribution」のコンテンツ(QuickTime Movie)を用いて説明しました。これはwebでアクセスできますので、各自で復習してください。
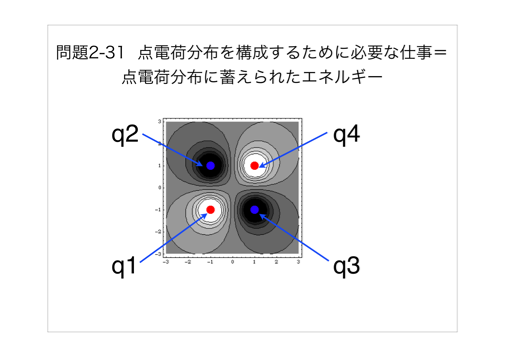
印刷できるようPDF版も置いておきます。
(6)点電荷分布に蓄えられるエネルギーの表式の和を積分に置き換えることにより、連続分布に蓄えられエネルギーの表式を導入したところで時間切れです。次回は、連続電荷分布によるエネルギーの表式(2.43式)を電場によるエネルギーの表式(2.45式)に書き換える話から始め、p96の導体(Conductor)に入ります。
5月15日(第5回目)の講義では
(0)今回の授業LOGは書き込みが遅れてしまいました。
(1)点電荷分布に蓄えられるエネルギーの表式(2.42式)から連続分布に蓄えられるエネルギーの表式(2.43式)を和を積分に置き換えることにより導入ししましたが、この2者の表式には質的な違いがあります。連続電荷分布によるエネルギーの表式(2.43式)をさらに電場によるエネルギーの表式(2.45式)に、テキスト(p93〜94)に従い、書き換えましたが、電場によるエネルギーの表式(2.45式)を用いるとその質的な違いが、はっきりします。


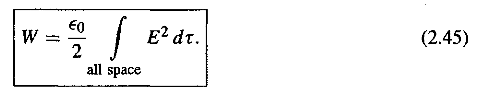
(2)その典型例として、2個の(正負の)点電荷からなる系のエネルギーを「点電荷分布に対するエネルギーの表式」で計算すると負の値になるが、「電場によるエネルギーの表式(2.45式)」を用いて計算すると常に正になり矛盾している?というパラドックスを示し、どうしてか?を発問しました。
「点電荷分布に対するエネルギーの表式」が点電荷(分布)を作るために必要な点電荷の(発散している)自己エネルギーを除いた表式になっていること、それが丁度「電場によるエネルギーの表式(2.45式)」における各点電荷が作る電場のCross-Termに対応していることを計算を通して説明し、「一見した矛盾」の謎解きをしました。これについては、テキストでは「p95 2.4.4 Comments on Electric energy」で言及しています。
(3)なお、「連続電荷分布によるエネルギーの表式(2.43式)」と「電場によるエネルギーの表式(2.45式)」は等価ですが、積分領域については、前者は電荷分布存在領域であり、後者は全空間であることに注意してください。この等価性については、問題2.32(a)&(b)を例にとり話しました(具体的な積分は各自で確かめてください)。またExample2.8(p94)にも目を通しておくと良いでしょう。

(4)電場によるエネルギーの表式(2.45式)を見ると、電場自身はこれまで学習してきたように重ね合わせ(superposition)が成り立ちますが、電場のエネルギーは重ね合わせが成り立ちません(No superposition)。その理解のcheckとして問題2.34をassignment#3(問題その1)として予約しました(半径aおよびbの球殻が持つ自己エネルギーは?、Cross-Termは?、No superpositionは?に注意して単なる計算に留まらないよう、読んでわかる解答を準備してください)
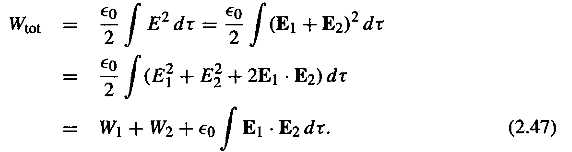
(5)p96の導体(Conductor)に入り、静電場のもとでは導体が満たすべき著しい性質(i)~(v)があること、またそれがどうしてか?について解説しました。これらの性質を前提にすると、導体内に作られたCavityについて特筆すべき性質が二つ現れることを話し始めました。
(6)第1番目は、外部電場の電気力線が導体の内部に侵入しないように電荷が表面に誘導され、これらの電気力線を吸収し外部電場からCavity内部が遮蔽される[静電遮蔽]ことです。MIT Open Course Wareで公開されている電磁気のVideo Lecutre5の 43分〜)を参考に見てもらいました。ここで時間切れです。

(7)次回は、もう一つの「導体内に作られたCavityについて特筆すべき性質」の話をして、2.5.3 Surface Charge and Force on a Conductorに進みます。
(8)Assignment#3は次回5/22(火)に2問目を出して課題とします。よって5/21(月)は提出日ではありません。
5月22日(第6回目)の講義では
(0)「導体内に作られたCavityについての特筆すべき性質」の1番目[静電遮蔽]を実感してもらうため、MIT Open Course Ware電磁気のVideo Lecutre5の 47分〜)にあるFaraday Cageのデモを見てもらいました。静電場ではないですが、Faraday Cageの中に一緒に持って入ったAMラジオは電波が遮蔽されて聞こえなくなる一方で、より高い周波数帯を使っている無線マイクはそのまま聞こえている点は面白いと思ったでしょうか?このあたりは9章で電磁波について学習するとわかるようになります。

(1)「導体内に作られたCavityについての特筆すべき性質」の第2番目として、帯電していない導体内のCavity内部に電荷を置いた場合には、『The conductor conceals from us all information concerning the nature of the cavity......』となることを説明しました。example 2.9(p99)を参照してみてください。all information とありますがCavity内部に置いた電荷の全電荷量は外からでもLeft overされた表面電荷の総量からわかります。
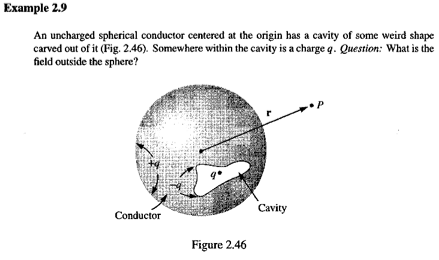
(2)第1番目の例を「Cavity内部は外から守られている」というならば 第2番目の例は逆に「導体内のCavityは外に対して隠される』と言えます。
(3)2.5.3 Surface Charge and Force on a Conductorに入り、任意の形状を持つ導体内部の電場をすべてゼロにするように表面電荷分布を決める『計算問題』は非常に複雑ですが、導体は物理法則に従い、あっという間にその『計算問題』を解いている点を強調しました。
(4)導体表面の電荷密度は曲率の大きい(小さい)ところで高く(低い)ことを、十分に離れているがワイヤーで同電位に保たれた半径の異なる2個の球状導体の計算例で示しました。その実例をMIT Open Course Wareで電磁気のVideo Lecture6の 6分〜で見てもらいました。導体でとがっている(曲率の大きい)部分は電荷密度が高く電場が強いため放電し易くなります。

(5)Force on a Conductorに話を移し、Local Patch以外の部分の作る電場(E other)はLocal PatchのOutside/On/Inside側で不連続性を示さないことを(解りやすいように定量的に電場の計算が出来ている球状導体を用いて)説明しました。Local Patchの作る電場の不連続性を、Total電場から取り除き E other を求めるための操作がp103に書いてある E above と E below の平均を取ることに対応します。なお、Local Patch自身が作る電場の不連続性のエッセンスは問題2.6の中にあります。このE other がLocal Patchに及ぼす力を求めることにより、ElectroStatic Pressureの表式を導出しました。
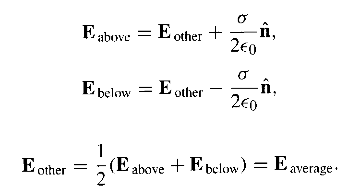
(6)ElectroStatic Pressureの別の導出を、仮想変位を考えたとき圧力がした仕事は電場の満ちている空間の減少によるElectroStatic Energyの減少分に等しいという関係から行いました。この考え方からも、静電エネルギーは「電場」に蓄えられていると実感できるでしょうか?ちなみに問題2.40(b)ではAlternative derivation of Eq. 2.52 と記述がありますが、この考え方にそっています。解いてみましょう。
(7)Assignment#3(その2)をMIT Open Course Ware電磁気学VideoLectureの8( 42分〜)を使い出しました。料理鍋の外側から電荷を与えると料理鍋の電位は直ぐに飽和してしまい電荷を移すことが出来なくなってしまいますが、鍋の内側から電荷を与えると電位は直ぐに飽和することなく(空気中でコロナ放電が起こるまでの電位になるまで)電荷を移すことができることを見てもらいました。これはVan de Graff 発電機の動作原理に他なりませんが、どうしてこのようなことが起きるか?を自身の言葉で書いてください。
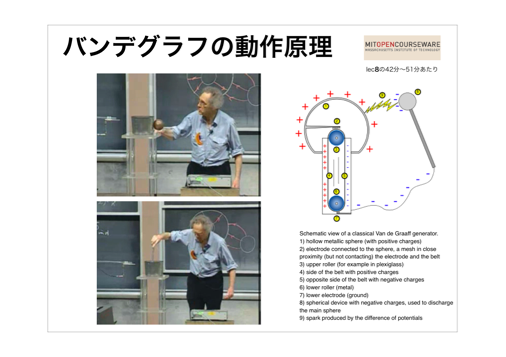
(8)静電容量Cの話をp105の例題2.11を用いて話そうとしたところで時間切れです。
(9)5月21日(月)〜6月1日(金)が「授業改善のためのアンケート」の学生回答期間ですので、回答をお願いします。
(10)次回は、静電容量について、導体の形状と相互の位置で決まる容量係数Cij まで話してから、5章に移り、静磁場に入ります。
5月29日(第7回目)の講義では
(1)Van de Graff 発電機の動作原理に直結するAssignment#3「その2」の解説をしました。そこでは、外部から接触させて電荷を移す方法に比べて、内部から電荷を移す方法が如何に効果的であるか?前回話した「導体内に作られたCavityについて特筆すべき性質」がどのように重要であるか?について強調しました。University Physics(11th edition)のp856にあるFaraday's icepail experimentも読んでみると参考になると思います。
(2)電場に蓄えられたエネルギーに関するAssignment#3「その1」では、電場については superposition E(total)=E(外側 shell)+E(内側Shell) が成り立ちますが、それらの自己エネルギーについてはsuperposition W(total) = W(外側 shell)+W(内側Shell) が成り立たずCross-Termも必要であることをふまえ、積分範囲を確認する程度に止めました。
(3)静電容量Cの話を例題2.11にそって解説しました。コンデンサーは電荷を蓄積するデバイスですが、電荷導体の形状と相互の位置で、電荷の蓄積の仕方がことなるはずで、それらを表すために必要になる容量係数C11,C12,C21,C22を導入し、静電容量Cとの関係(C={C11C22-C12^2}/{C11+C22+2C12})を与えました。テキストにはこれに関する記述はありませんが、電磁気学のミニマムとして必要だと思いましたので追加しました。
Assignment#4「その1」はC11,C21の具体的な計算、「その2」ではC12,C22の具体的な計算をして、求めた容量係数C11,C12,C21,C22の表式を(C={C11C22-C12^2}/{C11+C22+2C12})に適用して得られるCの表式が例題2.11のCの表式と同じになるか?をcheckするものです。
(4)2章を終え、5章の静磁場に移りました。電荷が移動しその流れである電流が生じる場合には、高等学校で習ったように磁場が発生しますが、この5章では定常的な電流の作る静磁場について考えます。Wireを流れる電流の定義=The current in a wire is the charge per unit time passing a given point に従い電流を担う電荷担体の正負については電流に作用する力では区別できないが、Hall effect(問題5.39 p 247)では区別が可能という話をしました、導線では電流を担うmobile negative charge(電子)とStatinary positive charge(イオン)があり電気的には中性であり、導線を流れる[定常]電流は外電場にさらされても力を受けない事を述べておきました。
(5)点電荷間に働くクーロンの法則を「電場の表式」と「その電場のもとで電荷が受ける力の表式」に分けたように、電流Loop間に働く力の法則(本来はアンペールの[力]の法則と呼ばれていたが、現代のテキストでは名前なしです)を「電流Loopの作る磁場の表式(ビオザバールの法則)」と「その磁場のもともう一方の電流Loopが受ける力の表式」に分けました。このアンペールの[力]の法則は一見、作用反作用の法則を満たしていませんが、問題5.49(p250)にあるように、Loop積分を実行した後は作用反作用の法則を満たしていることを確かめました。F12=-F21が自明に見えるこの表式はNeumann(ノイマン)の公式と呼ばれています。
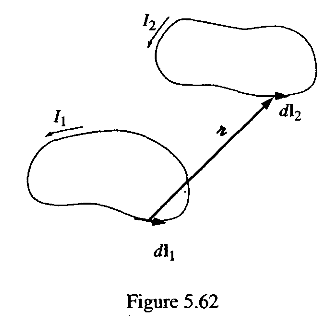
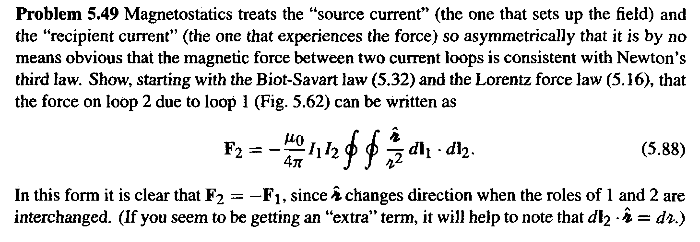
(6)次回はテキストにそって、2本の平行電流に働く単位長さあたりの力を用いて、電流の1Aを定義する話から始めて(p216)、定常電流(p208)、∇・B and ∇×B (p221)に進み、静電場の問題におけるガウスの 法則と同様に静磁場における有益な法則である「アンペールの法則」の話をします。
(7)5月21日(月)〜6月1日(金)が「授業改善のためのアンケート」の学生回答期間です。まだの人は回答をお願いします。
6月5日(第8回目)の講義では
(1)Assignmnet#4の解説をしました。容量係数C11,C21の計算を、電荷Q1,Q2を設定して、電荷分布の球対称性を満たすポテンシャルV(r)を書き出し、ポテンシャルV(r)の満たすべき境界条件 V(b)=0, V(a)=V1,V(∞)=0 を課してQ1∝V1, Q2∝V1の関係式を導き出し、その比例係数として、容量係数C11,C21の表式を得ました。
このようにして求めた容量係数C11,C21,C12,C22からC={C11C22-C12^2}/{C11+C22+2C12})により定義される静電容量Cは例題2.11の静電容量Cと一致したでしょうか?
(2)導体の電位を指定した際に、導体に誘起される電荷を表すために、容量係数C11,C21,C12,C22が定義されましたが、逆に導体に与える電荷を指定した際に、導体が持つ電位を表すために電位係数P11,P12,P21,P22が定義され、Cijを要素にもつ行列Cは、Pijを要素にもつ行列Pの逆行列になっていることを説明しました。(PC=CP=1)
さらに、導体の形、相互の位置関係という幾何学的因子だけで決まる容量係数、電位係数を用いて、導体系に蓄えられた静電エネルギーWが、電位Vあるいは電荷Qに関する二次形式で表されることを説明しました。
問題2.34では内側の球殻に+Q、外側の球殻にーQの電荷を与えたときの静電エネルギーを計算しましたが、Assignmentで求めたCijを用いて、その逆行列Pijを求め、W=1/2(P11*Q1*Q1+P12*Q1*Q2+P21*Q2*Q1+P22*Q2*Q2で静電エネルギーを計算して、問題2.34と同じ結果を得るか? 試してみると、さらに理解が進むと思います。
(3)2本の平行電流に働く単位長さあたりの力を用いて、電流の1Aを定義する話をしました。SI系ではまず電流がありきで1[A]=1[C/s]で電気量が定義されます。(高等学校で既に結果を知っている直線電流の作る磁場はp216例題5.5にありますが、これは読めばわかりますので各自で見ておいてください。)
(4)磁場Bの名前について、Bは「磁束密度(magnetic flux density)」で「磁場の強さ」Hと区別するよう高等学校でならったと思いますが、現在の電磁気学のteachingにおいては『Bを単純に磁場(magnetic field)と呼び、後半の6章で磁性体を含む静磁気学を論ずる際に導入する 補助場 Hは名前を付けず、ただHと呼ぶ』というコンセンサスがあります。
(5)ビオザバールの法則は定常電流が作る磁場を与える法則ですが、その定常電流の条件である∇・J=0について(電荷のLocal conservationを表す)連続の方程式(電荷保存の方程式とも言います)を用いて、話しました。
電流の定義が、電流を担う電荷担体が移動する経路が一次元的なwireの場合からどのように拡張されるか?その際にどのような面で積分するのか?についてsolenoid場∇・J=0であるため is independent of surface, for any given boundary line (面を定義する淵のLoopの形が決まれば、金魚すくい型でも虫取り網型でも同じ!)となることを強調しました。このあたりの数学定理が怪しい人は、p54 定理2を復習してください。
(6)点電荷の作る電場を重ね合わせて電荷分布の作る電場の表式を得たように、line currentの作る磁場を重ね合わせて体積電流密度Jを含む磁場の表式(ビオザバールの法則)5.39式 を書き出しました。定常電流の一部を取り出した部分電流要素については実在する電流としての意味を持ちませんが、その磁場への寄与を見るという点で意味があります。一定速度で動く点電荷については5.40式のような磁場を考えてしまいそうですが、これはもはや定常電流ではなく、定常磁場を表すビオザバールの法則は適用できません。正しい答えは10.68式&10.69式のようになります。(電磁気学の時間にはカバーできないので、3年生で電気力学の講義を聞いてください)。
(7)電流密度 J による磁場の表式(ビオザバールの法則)について∇・B、∇×Bを計算し始めました。
計算を始める前にB=∇×Aのように、あるベクトル場AのRotationで磁場Bが表現できる形に変形し進める点が、テキストと少し異なります(ちなみに、このベクトル場Aはベクトルポテンシャルと呼ばれるもので、すぐあとに出てきます)。
(8)次回は、B=∇×Aの表式に対する∇・B および ∇×Bの計算から始まりますが、計算は少々技巧的で退屈かと思いますので、PDFファイル2007-6-5AUXmemo.pdf(A4一2枚)に∇×Bの計算を書いたものをwebにUPしましたので、ダウンロードして、さっと目を通して、次回に持ってきてください。
2007-6-8
Web授業アンケート(2007年度1回目)に対する回答を掲載しました。
6月12日(第9回目)の講義では
(1)電流密度 J による磁場の表式(ビオザバールの法則)から出発してそのDivergence ∇・B と Rotation ∇×Bを計算する話から始めました。 PDFファイル2007-6-5AUXmemo.pdf(A4一2枚)にあるように、やや技巧的ですが∇×Bの計算を進めると、∇×B=μ0*J+2nd Term という形にまとめることができ、∇・J=0を満たす定常電流の場合は2nd Term は消えて、アンペールの法則(微分型)∇×B=μ0*J を得ることができます。さらに、これをストークスの定理を用いてアンペールの法則(積分型)に変えると、静電場の問題におけるガウスの 法則と同様に静磁場を求める上でパワフルな法則になります。
(2)脇道にそれましたが、定常電流でない場合を考えると、連続の方程式を用いて2nd Term内の被積分関数∇・J を電荷密度の時間変化に置き換え整理することで、『見かけ上』、2nd Termがいわゆる「変位電流項」に化けて、p326 の7.39式にあるMaxwell方程式の4番目自身が出てくる話をしました。『見かけ上』と言っているように、Biot-Savartの法則は定常電流が流れている場合に成立する法則であり、非定常電流が流れている場合に成立する磁場の表式は(拡張されたBiot-Savartの法則である)Jefimenko 方程式(p428の10.31式)になります。7章にはいってまた言及しますが、webコンテンツ「変位電流は磁場をつくるか?」の中にある『Biot-Savartの法則からAmpere-Maxwellの法則は導けるか?』
を見ておいてください。
(3)アンペールの法則(積分型)のパワフルさとアンペールの法則(微分型)という場の方程式 ∇×B=μ0*J の意味を確認するためにAssignment#5を出しました。
Assignment#5(その1)は、授業で解説したp227のExample5.9(Solenoid Coil)では半径Rの円筒形に巻かれたコイルを考えていますが、その断面が円形でない(金太郎飴のようにどの場所でも断面の形は同じ)Solenoid Coilを同様に想定し、コイルにより作られる磁場を求めることです。
Assignment#5(その2)は、半径aの円柱を軸方向に一様に流れる電流分布(全電流をIとする)の作る磁場を求め、その磁場がすべての点で場の方程式 ∇×B=μ0*J を満たしていることをcheckせよという問題です。
(4)電場をガウスの法則を用いる際と同じ様に、アンペールの法則(積分型)は常に正しいが、usefullなのは電流分布の持つ高い空間対称性に起因する磁場の呈する空間対称性があるときだけであることが、授業で話した、p226のExample5.7(直線電流)や p227のExample5.9(Solenoid Coil)で体感できたでしょうか? その意味で、上記の「その断面が円形でない(金太郎飴のようにどの場所でも断面の形は同じ)Solenoid Coil」でもまだ高い空間対称性があるので、アンペールの法則(積分型)を利用できることになります。
(5)Example5.8(Current Sheet)、問題5.14(Slab),問題5.15(2重のSolenoid Coil)を演習時間に解いてみてください。
(6)静電場と静磁場について場の方程式の違いをもとに、定性的にどのような違いがあるかを話しました。もしMagnetic monopole(磁気単極子:磁荷)があれば、∇・Bの右辺にそれが現れ、磁荷の流れに対応する磁流が∇×Eの右辺に現れ、静電場と静磁場は全く対称になることを話しました。電荷の流れに対応する電流が∇×Bの右辺に現れるが、磁荷がないからこそ、電荷の流れの効果が、相対論効果で小さいながらも、磁場として見えていると言えます。「相対論効果としての磁場」は大変面白い話で物理学科の皆さんはきっと早く話が聞きたいと思いますが、後期までお楽しみに!
(7) 次回は、5.4.1 Vector Potential、5.4.2 Magnetostaic Boundary conditionsを話して7章の7.1 Electro Motive forceに入ります。
6月19日(第10回目)の講義では
(1)Assignment#5の解説をしました。前回の講義での話をもとに各自の言葉でまとめる内容でしたので全体的に良く出来ていました。
その1では、その断面が円形でない(金太郎飴のようにどの場所でも断面の形は同じ)Solenoid Coilの問題ではどのような「磁場の呈する空間対称性」がある故、アンペールの法則(積分型)を利用できたのか?がはっきりしたでしょうか?
その2では、電流分布 J 、電流分布の内部および外部の磁場 B 、および場の方程式 ∇×B=μ0*J の関係が体感できたでしょうか?
(おまけ)先週話した2B学生実験題目「音の分析」に関係した話を少ししました。実際に試してくれた人もいたように、実験室に行かなくてもWebの上で試せます。是非、試して、さらなる「面白そうな?」問題設定を考えてみましょう。
(2)5.4.1 Vector Potentialに進み、
Vector Potential A の話をしました。あるスカラー場λのgradient∇λを加えるゲージ変換を行っても同じ磁場Bを与えるゲージ不変性があるため、種々のゲージの取り方が可能であることを話しました。ヘルムホルツの定理からは場 A を定めるために∇×Aと∇・Aの両方を定める必要がありますが、∇×Aについては文字通り∇×A=Bとして指定されていますが、∇・Aについては何も言っていないため、このような任意性が生じます。考える問題に適したゲージ(ローレンツゲージ、放射ゲージ、etc)を設定することができますが、静磁場では∇・A=0となる『クーロンゲージ』と呼ばれるゲージが適しています。
『 6月12日(第9回目)の講義(1)』では電流密度Jによる磁場Bの表式(ビオザバールの法則)をB=∇×Aのように、あるベクトル場AのRotationで磁場Bが表現できる形に変形して話を進めましたが、まさにこのベクトル場 A がVector Potential A の表式になっています。Vector Potential Aの表式(式5.63)がクーロンゲージを満たし、B=∇×Aにより、磁場Bの表式(ビオザバールの法則)を与えることをcheckする問題5.27(a)&(b)を各自で解いてください(答えは2007-6-18AUXmemo.pdf(A4一1枚)PDFファイルを参照)
(3) Vector Potentialの実際の計算例として、ソレノイド電流のつくるA(r)を例題5.12 に沿い求めました(ここでは、アンペールの法則[積分型]とのアナロジーを用いた論理展開をしていますが、授業で話したようにVector Potentialの方向が電流と同様にφ方向にあることをAの表式(式5.63)から吟味するプロセスをきちんと踏んでください。
ソレノイドコイルの外側には、運動する荷電粒子に力を及ぼす物理的実体である磁場Bがないにも関わらず、Vector Potential A(r)は有限の値を持ちますが決して意味のないものではなく(その昔は電場や磁場の計算に便利な数学的な補助量と思われていた)、電子の波動関数の位相のずれとして影響する物理的実体であり、それがアハラノフ・ボーム効果(AB効果)として予言され、干渉実験を通して実証されていることを述べました。
ベージ全体
http://www.i-eng.hitachi.co.jp/column/tuika/tonokouen.htm
を読んでみると面白いと思います。
(4) Vector Potential自身は電位のように実用上有効な物理量でなく、かつその物理的な意味付けが簡単ではありませんが、上述したアハラノフ・ボーム効果に見られるように概念的には非常に重要な量です。
Vector Potentialの実際の計算例として、例題5.11(p236)[回転する球面電荷(球殻内はω方向を向いた一様な磁場が出来ている[p240 問題5.29]]、問題5.22(p239)[直線電流]、問題5.26(p239)[Current Sheet]を演習時間に解いください。
(5)静電場において、「電荷分布ρ」vs「電場 E」vs「Potential V」の関係を図式化(図2.35)しましたが、対応して、静磁場について「電流分布J」vs「磁場 B」vs「Vector Potential A」の関係を図式化(図5.48)しました。「Vector Potential A」to 「電流分布J」に現れるVector Potential Aについてのラプラス方程式のラプラシアンについての注意(p235 FootNote 13)を言及しておきました。「磁場 B」 to 「Vector Potential A」のmissing lineについては問題5.50&5.51を言及しておきました((ii)のソレノイド場についての公式はベクトル解析のテキストを参照すると良いでしょう))
(6)なお、p241-242にあるMagnetostatic Boundary conditionsの話はしていませんが、関連する話が出た時に戻って話します。
(7)次回からは7章に移り、時間的に変動する電場/磁場の話に移ります。その導入として、p293の問題7.6(図7.9)を来週まで考えてみてください。永久機関こたつは作れますか?
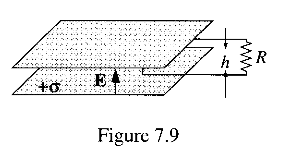
来週は7.1.2(p292) Electromotive Forceの話から始めます。
6月26日(第11回目)の講義では
(1)先週考えて見てくださいと振ったp293の問題7.6を解説しました。回路中の単位電荷に作用する力がする仕事として定義されるEMF(Electro motive force)は、∇×E=0の条件を満たす静電場については、ゼロになり、永久機関「こたつ」はできません。静電場の満たす保存場∇×E=0の条件は結構な条件であることが体感できたでしょうか?
(2)2006年度も言及しながら時間の都合で話ができませんでしたが、コンデンサーの端の複雑な電場は、複素関数論における等角写像を用いて求めることができます。今年度は時間が取れれば話します。
(3)p295にある「Although the magnetic force is responsible for establishing the EMF, it is not doing any work. Who is supplying the energy? 」「The person who is pulling on the loop !」は講義を聞いて納得できたでしょうか?
単位電荷に働くローレンツ力fmag自身は全く仕事をしませんが、ローレンツ力が媒介するこにより水平右方向にagentの加えた力fpullがredirectされ垂直上方向に回路に沿って単位電荷を駆動していることになります。これは、p209例題5.3の最後あたりにあるIt may help to consider a mechanical analogy....と同じで、水平右方向にagentの加えた力fpushが直接、物体を持ち上げているわけではないが、仕事を全くしない垂直抗力Nが媒介してIt redirects the efforts of active agant from horizontal to verticalの状況と同じであると言えます。それゆえemfの定義に従った計算(7.11式)を行うことにより、(emfにはまったく寄与しない)力fpullが(起電力と見なされる)単位電荷にした仕事(vBh)が求めるられることになります。
高校の時使った物理IIの教科書を開いて、これらの事情がどう記述してあるか、批判的に見てみると面白いと思います。
(4)マーキングして返却はしませんが、Assignment番外編を出しました。上記の例において「斜面の登る物体に働いている重力に相当する力は、このEMFの問題では何になるでしょうか? 答えだけ「....の力」と書くのではなく、いつもの提出用紙1枚に、Self-containedで(それだけを読んで、お話が分かるように)書いてください。次回の講義時に解説し、これをもとに「電流を担っている電荷の速さが如何に遅いか!」について話をします。回収BOXは7/2にNo1が出ます。
(おまけ)物理学科のFDの一環で、録画した授業を「授業者自身の振り返り」および「学科スタッフ間の相互参観」に活用する試みを主に後期に行う予定ですが、試しに、録画してみました。以下はそのスナップショットです。(授業を聞かなかった人には)Assignment番外編を考える際に足しになるかもしれません。
録画を見ると、喋り方がなっていないのがよくわかります。また来週も取ってみる予定です。
(5)テキストp296に沿い、磁気力(ローレンツ力)によるMotional EMFを磁束の変化率で表現するFlux Ruleを一般的に証明しました。この段階ではファラデーの法則(EMF=-dφ/dt)とは何の関係もありません。
(6)テキストp301に移り、実験(1)の結果はMotional EMFによるものでMagnetic originであり、実験(2)の結果は相対運動を考えると当たり前のように思えますが、変動する磁場により誘起された電場(ファラデー電場)によるものでElectric originであり、メカニズムが全く異なる!?にもかかわらず両者がε=ーdφ/dtという一つのFlux Ruleで書けることは驚きであることを話しました。実際Einsteinはこれが単なる偶然の一致であるとは信じがたく、これを1905年の特殊相対性理論の論文の導入部で述べています。と言う訳で、相対論と電磁気は不可分であるという要素があり、後期に開講される相対論は是非、聞いてください。
(7)次回は、p305の7.2.2 Induced Electric Field の続きを話して、変位電流(p321〜)に進みます。変位電流は電磁気学でも大変面白い部分ですが、難解な部分でもあります。時間のある人は、以下のwebマテリアル「変位電流は磁場をつくるか?」を眺めてみてください。次回の講義ではここで用いている平行円板コンデンサーへの充電過程を用いて、変位電流の話を進めます。
(8)7/24(14回目)が最後の授業の予定ですが、前期試験の前日であり、7/17は月曜の授業用に振替なので、7/3(12回目)、7/10(13回目)に続き、7/14(土曜日)午後に補講時間を設定し、最後の14回目の授業とします。(生物学実験で問題がある可能性を指摘した人は、今週中にそれを確認してメールで教えてください)
7月3日(第12回目)の講義では
(0)Assignment番外編の解説をしました。電気抵抗の話に続けるつもりでしたが、実験室で見かける実用的な電流を流している状況(断面積1[mm^2]のCu(銅)線に電流(1[A])を流している)における電子の速度vを求めて、それが如何に遅いかを解説するに止めました。オームの法則についてはあとで説明します。

(1)静電場(クーロン電場)と異なり、場の方程式(∇・E=0,∇×E=-∂B/∂t)を満たす、変動する磁場によりinduceされた(ファラデー)電場を理解してもらうため、ソレノイド電流が時間に比例して増大している状況を考え、一定の時間変化率を持つ円柱状の一様な変動磁場により、時間変化しない電場が誘起されることを説明しました。その空間分布は、一様な定常円柱電流により作られる磁場の空間分布と(向きが逆を除けば)同じになります。
(2)p321に移り、「定常電流に対する」という付帯条件のついたアンペールの法則(微分型)∇×B=μ0J(式4)は非定常電流の場合に成り立たないことを、数式の上でそのInconsistency を説明し、一定電流によるコンデンサーの充電過程の例(これは定常電流でなく非定常電流になっている!)を用いて、アンペールLoopを淵に持つ曲面の選び方により議論が混迷する例により、確かに矛盾があることを話しました。定常電流では、ワイヤーの途中で電荷が蓄積されることはありませんでしたが、ここではコンデンサーの極板上に電荷が貯まっています。「非定常電流に対しては、the current enclosed by a loop is an ill-defined notion (p322)です
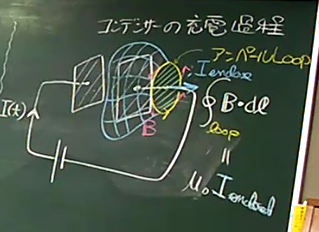
(3)アンペールの法則に新たに変位電流項を加えたアンペールの法則(with Maxwell's correction)では、そのInconsistency が解消されていることを説明しました。変位電流はその名前が「電流」となっていますが、電荷が移動する「真電流 J 」とは何の関係もなくMisleadingな名前です。Maxwellが変位電流と名前を付けたのは誘電体における分極電流(後期に解説します)とのアナロジーがあります。時間変化する電場のもとでは、誘電体に誘起される分極が時間変化し分極電流が生じますが、Maxwellは真空自身も誘電体と同様に振る舞う、ある種特別な誘電体(エーテル)であると考えて、対応する分極電流(変位電流)が流れると考えていたそうです。 最近は、時間の都合で見せていませんが、MIT Open Course Ware電磁気学VideoLectureの18( 22分〜23分)あたりを是非見てください。実験のデモではありませんが、変位電流の名前の由来と、Misleadingな名前ではあるがこの項の重要性自身は変わらないことを、Romeo and Julietに出てくる有名な台詞"What's in a name? That which we call a rose by any other name would smell as sweet."を使って説明しているのが印象的でした。全然関係ありませんが、Star Trek (宇宙大作戦)TVシリーズの中の秀作だと思うエピソード「by any other name」のタイトルもRomeo and Julietから来ています。

(4)現代的なテキストは「変位電流項」よりは「Maxwell項」と呼ぶほうが適切であると述べています。その意味でファラデーの法則(∇×E=-∂B/∂t)の右辺は「ファラデー項」と呼ばれていますが、「変位磁流項」とは言いません。(この点については次回にまた言及します)
(5)変位電流を導入すると、どのように、上記(2)の混迷が解消されるかを、p323 下から2行目〜p324「Let's see now how the displacement current resolves .....にあるように、次に解説すべきでしたが、急いで飛ばしてしまいました(目を通しておいてください)。
(6)p324のproblem7.32にあるようにコンデンサー極板内に作られる磁場をアンペールの法則(with Maxwell's correction)を用いて計算しました。そのfoot note14(This problem raises an intersting quasi-philosophical question)」にあるように、コンデンサー内の磁場を測定すると、
変位電流の効果を見ていることになるのか?
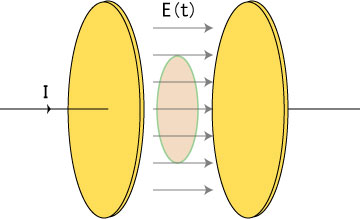
単に電流の効果を見ていることになるのか?
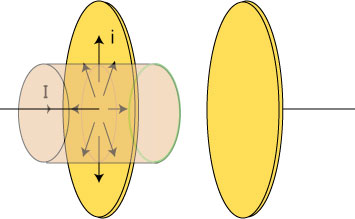
どちらなのか? 不思議な疑問が生じますねと話を振りました。コックさん帽子の側面からのout-going電流の表式をI*(1-(s/a)^2)と与えましたが、説明がいくらか雑なところがありましたので、自作webマテリアル「変位電流は磁場を作るか?」を見て、補っておいてください。
(7)次回は、今回の補足をしたあと、p326から
7.3.3 Maxwell's Equations, 7.3.4 Magnetic chargeに進みます。
(8)今回の授業は、授業開始直前まで3時間近くかなり頭を使う会議をしてお昼抜きだったためか、(動画記録を見ながらLOGを書いてみて良くわかりましたが)仕上がりが良くない状態でした。やはり、直前には時間を取ってウオーミングアップをすることが必要だと思いました。
(9)アナウンスしたように、次回、7/10(13回目)に続き、7/14(土曜日)午後12:50〜16:00(恐らく15時過ぎには終えられると思います)941教室で最後の14回目の授業とします。(7/24は授業はありません)
7月10日(第13回目)の講義では
(1)先週、説明が雑であった「変位電流を導入すると、どのように、混迷が解消されるか」について、先週扱った問題7.32(p324)より簡単な状況設定を用いた問題7.31(p324)を用いて説明しました。
(2)テキストp326-327に沿って、実験事実から積み上げて来た電磁現象を記述するMaxwell方程式(式7.39)について話しました。テキストには書いてありませんが、Maxwell方程式を、電磁場の時間発展を定める(運動方程式に相当する)式7.39の2組(iii)と(iv))と、補助条件(運動の初期条件に相当する)式7.39の2組(i)と(ii))とに分けて、その意味付けを考えました。Maxwell方程式は電場と磁場が絡んでいるため、「変化する磁場が電場をつくる」や「変位電流が磁場をつくる」といった表現を多くのテキストで見かけますが、何が電磁場の源であるか?という意味からは注意が必要であり、電場と磁場の絡みをほどいた(非済次)方程式を導出し、左辺には(電場/磁場)が空間と時間をどう伝搬するかを表すダランベール演算子が、右辺には電荷と電流がソースとして現れることを話し、電場と磁場のソースは電荷と電流であることを強調しました。
(「変位電流は磁場を作るか?」というwebマテリアルの「3.Jefimenko方程式」を参照してください)
(3)次に、7.3.4 Magnetic Charge(p327)の話をするつもりがすっかり忘れてしまいました。次回7/14に話します。
(4)問題7.11(p300)の解説をしました。運動方程式を無次元化する過程で考えているsystemを特徴付ける速度や時間のスケール(ものさし)が見える話はどうでしたでしょうか? 調和振動の運動方程式を無次元化する過程ではsystemを特徴付ける時間として(2πという因子程度は別にして)周期が見えました。特徴的な長さ(振幅)や速度は初期条件で決まり、運動の因果律を表す運動方程式の中に直接書き込まれているわけではありません。
問題7.11数を解くと、ミリ秒程度でほぼ終端速度に達する結果が出て来ます。これと同様な電磁制動の現象(テキストp299図7.15)をMIT Open Course Wareのvideo(Lecutre17の 40分目あたり)で次回7/14に見せます。
(5)次元解析とスケーリングに関連して、1945にNew Mexicoで最初に行われた原子爆弾の実験で、高速写真により記録された火の玉の半径Rの時間発展R(t)は以下の図のように、時間tのベキ則を示し、その指数は〜2/5=0.4ですが、このベキ則指数を、この系のエネルギー拡散過程を表す偏微分方程式を解かなくても、適当な仮定のもと次元解析を行うことにより出すことができます。
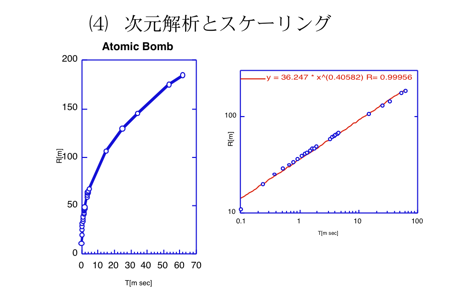
http://nsmsxserve02.ph.kagu.tus.ac.jp/1BPhysics/main.html
(6)テキストp310に従い、mutual-inductanceについて解説しました。その定義からはある意味当たり前に思えるM12=M21は以外にもAstonishingであることを体感してもらう例題(例題7.10の有限長と無限長の同軸ソレノイドコイルの問題)の話を始めたいところで時間切れです。
(7)アナウンスしたように、7/14(土曜日)午後12:50〜16:00(恐らく15時過ぎには終えられると思います)941教室で最後の14回目の授業とします。(7/24は授業はありません)
(8)7月2日(月)〜7月13日(金)が第二回目の「授業改善のためのアンケート」の学生回答期間です。アナウンスするのをすっかり忘れていました。まだの人は回答をお願いします。
7月14日(第14回目)12:50〜15:30?の講義では
(1)台風4号が近づいている土曜日でしたが、2時間強の間、補講授業ご苦労様でした。本日はもう元気が無いので簡単に書きます。
(2)How M12=M21 is astonishing を先週の続きで話しました。例題(例題7.10の有限長と無限長の同軸ソレノイドコイルの問題)を復習してください。
(3)Magnetic Brakingの話をMIT-OCWから見てもらいました。

(4)Magnetic Chargeの話をしました。Magnetic Charge(Magnetic monopole)はその存在が今日まで実験では見つかっていませんが、Maxwell方程式は電場と磁場の対称性からはMagnetic Chargeを請うていると言える話をしました。
(5)電磁誘導の話をMIT-OCWから見てもらいました。

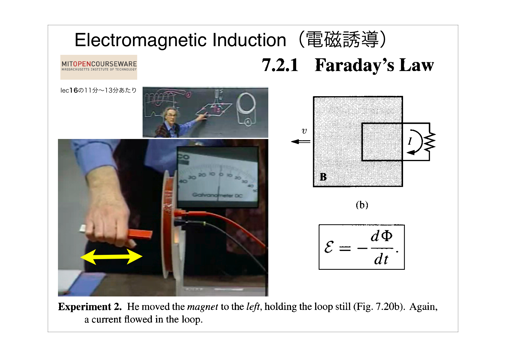


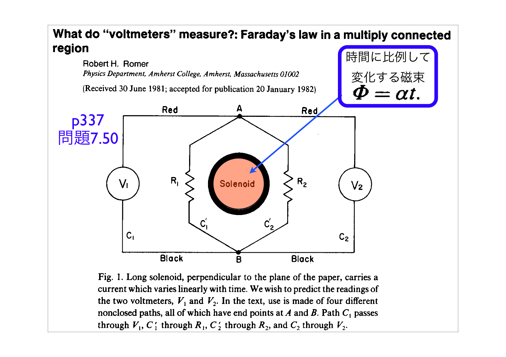
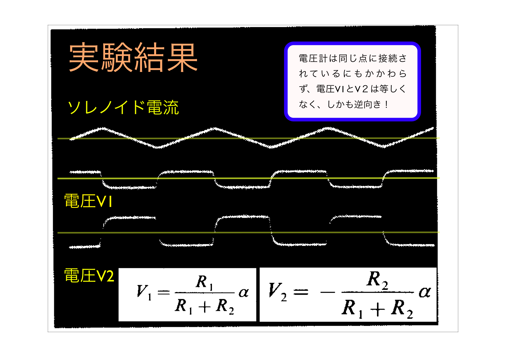
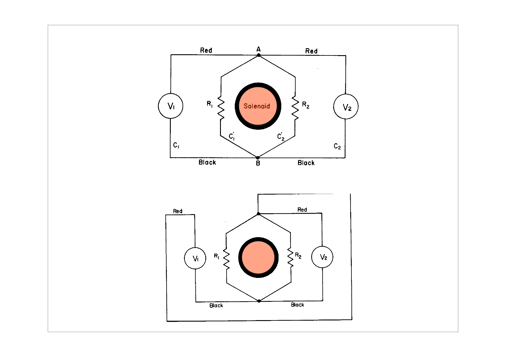
特に、時間変動する磁場が存在する場合は電場は保存場でなく、電位の概念は成り立たないことを理解してください。
(6)磁場に蓄えられたエネルギーの話を、テキストに沿って話しました。ソレノイド磁場に蓄えられたエネルギーを種々の表式にしたがい計算するp320問題7.26を各自でやってみてください。
(7)磁気浮上の話をMIT-OCWから見てもらいました。

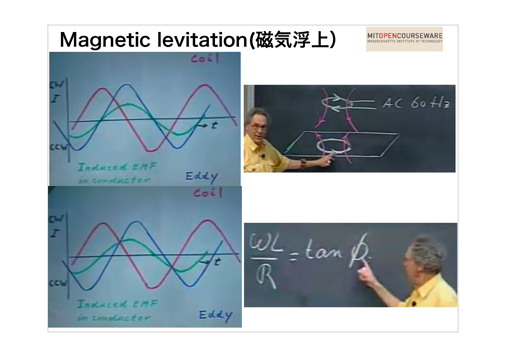

磁気浮上は結構意外だったのではないでしょうか?(最初に見たときは、え、と思ったのを覚えています)
(8)オームの法則、表面電流の裏と表における磁場の境界条件、等については時間切れですが、後期に必要になった時点でまた話します。
(9)7/31の定期テストについては授業中に述べたように、計算に惑わされず概念を正しく自身の言葉で表現できるように、しっかりと復習してください。
(10)7月2日(月)〜7月13日(金)が第二回目の「授業改善のためのアンケート」はアナウンスし忘れたためかもしれませんが、たった13人でした。サンプリング数が少ないですが、記録として、ここに保存しておきます。2007年度:第二回目の「授業改善のためのアンケート」結果
(11)夏休みの宿題は特には出しませんが、少し時間が出来たら、英語の勉強も兼ねて、前期に見せたMITオープンコースウエア(Physics:8-02Electricity-and-MagnetismSpring2002)のビデオlecture を見て味わい深い講義を楽しんでみてください。非常におすすめです。
では良い夏を過ごしください。
-----------
これで前期の授業はすべて終わりです。